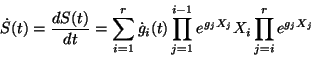Compute the right-hand side of the Wei-Norman formula:
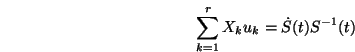 . .
|
Syntax e:=wne(r,max_bracket_order,X);
e:=wner(r,max_bracket_order,X,B,lbt);
Description
|
Computes the right-hand side of the Wei-Norman formula:
where  are indeterminate elements
independent of time that define a basis for an arbitrary Lie algebra,
and with are indeterminate elements
independent of time that define a basis for an arbitrary Lie algebra,
and with
 is required to be finite
dimensional. is required to be finite
dimensional.
The above expressions for 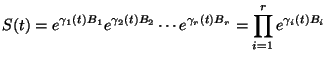 and and 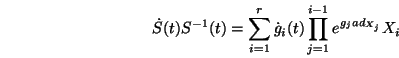 , together with the
exponential formula given in equation (9) allow to
express the right-hand side of the Wei-Norman equation as: , together with the
exponential formula given in equation (9) allow to
express the right-hand side of the Wei-Norman equation as:
Hence, this procedure can be implemented in a simple way in terms of the functions ead, eadr and pead, peadr. wner, reduces the Lie brackets in the expression to elements in the PHB, and further simplifies the expression according to the supplied Lie bracket table. If the Lie bracket table is an empty list or set, no additional simplifications are carried out. |
Arguments

max_bracket_order


wner additionally requires:


Examples
A similar calculation to the previous one, but with the assumption
that the bracket
> w5r:=wner(r,max_bracket_order,B,B,{B[6]=0});
w5r := dg1~ f0~ + dg2~ f1~ + (dg2~ g1~ + dg4~) (f0~ &* f1~)
2
+ (1/2 dg2~ g1~ + dg4~ g1~) (f0~ &* (f0~ &* f1~)) +
3 2
(1/6 dg2~ g1~ + 1/2 dg4~ g1~ )
(f0~ &* (f0~ &* (f0~ &* f1~))) + dg3~ f2~
+ dg3~ g1~ (f0~ &* f2~)
2
+ 1/2 dg3~ g1~ (f0~ &* (f0~ &* f2~))
3
+ 1/6 dg3~ g1~ (f0~ &* (f0~ &* (f0~ &* f2~)))
+ dg4~ g3~ (f2~ &* (f0~ &* f1~))
2
+ 1/2 dg4~ g3~ (f2~ &* (f2~ &* (f0~ &* f1~)))
+ dg4~ g2~ (f1~ &* (f0~ &* f1~))
2
+ 1/2 dg4~ g2~ (f1~ &* (f1~ &* (f0~ &* f1~)))
+ dg4~ g1~ g2~ (f1~ &* (f0~ &* (f0~ &* f1~)))
As expected, the difference w2r-w5r shown below contains only
terms of the bracket
3
+ 1/6 dg3~ g2~ (f1~ &* (f1~ &* (f1~ &* f2~)))
2
+ 1/2 dg3~ g2~ (f1~ &* (f1~ &* f2~))
+ dg3~ g2~ (f1~ &* f2~)
|
Note that an actual computation in Maple of 'w2r-w5r;'
returns an expression that contains terms, such as:
(-dg1~ + dg1~) f0 + + (-dg2~ g1~ - dg4~ + dg2~ g1~ + dg4~) (f0~ &* f1~) + ...that are not simplified to zero because each time wner is invoked, different variables dg1, dg2, etc., are created at each time (i.e. the variables have the same name, but they do not correspond to the same instance of a unique variable in the Maple space, in fact they are instances of different variables). Although this does not seem so far to cause significant problems, its is worth to mention that if one wishes to make comparisons between expressions it would probably be convenient to modify the routines wne and wner so that they declare variables g and dg in the global space as unique instances. |
See Also
ead, eadr, pead, peadr.
|
References
| See [32] and references therein for an explanation on the derivation of the Wei-Norman equations. |