



Next: phbize
Up: Function Reference
Previous: createLBobjects
Contents
Purpose
Generate a Philip Hall basis.
Syntax
B:=phb(m,k);
Description
This function constructs a list containing the Philip Hall basis (PHB)
for a nilpotent Lie algebra of degree 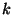 generated by generated by 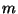 generators.
The elements in the PHB are elements of the Lie algebra selected in
way such that the dependencies between brackets, imposed by the
anti-symmetry property and the Jacobi identity, are taken into
account. generators.
The elements in the PHB are elements of the Lie algebra selected in
way such that the dependencies between brackets, imposed by the
anti-symmetry property and the Jacobi identity, are taken into
account.
|
Arguments
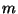 Number of Lie algebra generators.
Number of Lie algebra generators.
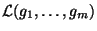
Examples
Construct a Philip Hall basis for a nilpotent algebra of order 4
generated by 3 vector fields.
> B:=phb(3,4);
B:=[f0~, f1~, f2~, f0~ &* f1~, f0~ &* f2~, f1~ &* f2~,
f0~ &* (f0~ &* f1~), f0~ &* (f0~ &* f2~), f1~ &* (f0~ &* f1~),
f1~ &* (f0~ &* f2~), f1~ &* (f1~ &* f2~), f2~ &* (f0~ &* f1~),
f2~ &* (f0~ &* f2~), f2~ &* (f1~ &* f2~),
(f0~ &* f1~) &* (f0~ &* f2~), (f0~ &* f1~) &* (f1~ &* f2~),
(f0~ &* f2~) &* (f1~ &* f2~), f0~ &* (f0~ &* (f0~ &* f1~)),
f0~ &* (f0~ &* (f0~ &* f2~)), f1~ &* (f0~ &* (f0~ &* f1~)),
f1~ &* (f0~ &* (f0~ &* f2~)), f1~ &* (f1~ &* (f0~ &* f1~)),
f1~ &* (f1~ &* (f0~ &* f2~)), f1~ &* (f1~ &* (f1~ &* f2~)),
f2~ &* (f0~ &* (f0~ &* f1~)), f2~ &* (f0~ &* (f0~ &* f2~)),
f2~ &* (f1~ &* (f0~ &* f1~)), f2~ &* (f1~ &* (f0~ &* f2~)),
f2~ &* (f1~ &* (f1~ &* f2~)), f2~ &* (f2~ &* (f0~ &* f1~)),
f2~ &* (f2~ &* (f0~ &* f2~)), f2~ &* (f2~ &* (f1~ &* f2~))]
|
Notes
This function also declares the symbol for the Lie product operator
denoted by &* if it was not previously assigned. This is only
to ensure that &* and its properties (see Loading LTP
in section 2.3 have been assigned in case it was
manually removed. The &* operator is created by default at
startup when the package is loaded.
|
Limitations
|
There aren't any known limitations, besides the normal limitations
imposed by the memory of the machine.
|
See Also phbize.
Algorithm
Implementation Notes
The implementation of the algorithm is illustrated in the flow chart of
Figs. . For further details and
remarks on the implementation the reader is referred to the source
code.
From a practical perspective, the basis B can be built in such
a way that only condition 3 needs to be checked, since condition 1
must be assumed true for all initial generators and 2 may be
satisfied by performing the multiplications in an orderly manner, as
briefly described next.
Condition 3 is implemented within the dashed block labeled ``Create
bracket ![$[B_i,B_j]$](img495.png) '', shown in Fig. 5. '', shown in Fig. 5.
The bracketing procedure (i.e. the procedure for generating new Lie
products or brackets) can be though of as a breeding process. We must
distinguish between to groups per ``breeding season'' (iteration), the
offspring and the parents.
On the first iteration the generators are treated as offspring
and are crossed between them. On the second iteration,
the offspring are called parents (since they will be crossed they will
become parents), and their offspring are the new offspring. Parents
are crossed only with their offspring and not between them, since this
happened in the previous iteration. While offspring are crossed between
them and also their parents to cover all possible combinations. All
the newborns are now called offspring and the ones that were offspring
are now in the group of parents. And life goes on...
Offspring are ``cross-fertilized'' as shown in Fig. 6.2.
|
Figure 3:
Lie bracketing tree.
|
|
Note that the [B,C], [C,A] and [B,A] are not valid offspring since
they violate condition 2, assuming a lexicographical order is followed,
i.e. A, B, C, are respectively the first, second and third generators.
Now there are two groups: parents A, B, C and offspring [A,B],
[A,C], [B,C], denoted AB, AC and BC for short. Offspring will
reproduce again as graphically described in the above figure, but also
they will be crossed with their parents. All parents are crossed with
all offspring, in the following way:
AxAB AxAC AxBC
BxAB BxAC BxBC
CxAB CxAC CxBC
Where 'x' stands for crossed with, i.e. represents the Lie product
operator. Note that some of the crossings must be eliminated by rule
3, namely AxBC.
In the flow chart of Figs. 4-5, 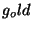 denotes
the bracketing iteration (breeding season), denotes
the bracketing iteration (breeding season), 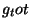 is the number of
brackets that have been multiplied (crossed) at least once, is the number of
brackets that have been multiplied (crossed) at least once, 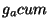 is
the number the total number of brackets including parents and
offspring updated at the end of the iteration. Note that is
the number the total number of brackets including parents and
offspring updated at the end of the iteration. Note that
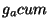 is note incremented as the breeding occurs since its value is
necessary to close loop L3, in Fig. 5, to keep track of
the new brackets the variable is note incremented as the breeding occurs since its value is
necessary to close loop L3, in Fig. 5, to keep track of
the new brackets the variable 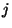 is used, instead, and its value
will be passed to is used, instead, and its value
will be passed to 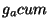 once the loop L3 is completed. The index once the loop L3 is completed. The index 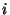 points to each element in the initial population, and is associated
with the first term in the bracket
points to each element in the initial population, and is associated
with the first term in the bracket ![$[B_i,B_j]$](img495.png) , while the index , while the index 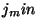 associated with the second term in the bracket is set to start at the
value of
associated with the second term in the bracket is set to start at the
value of 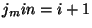 according to whether the the crossings will be done
between the offspring only ( according to whether the the crossings will be done
between the offspring only (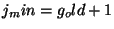 ) or between the parents and the
offspring ( ) or between the parents and the
offspring (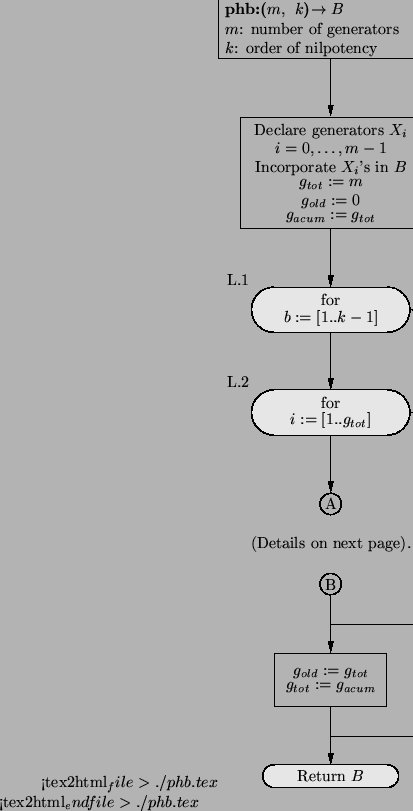 ). ).
|
Figure 4:
Flow chart for the phb algorithm (contd. on
Fig. 5).
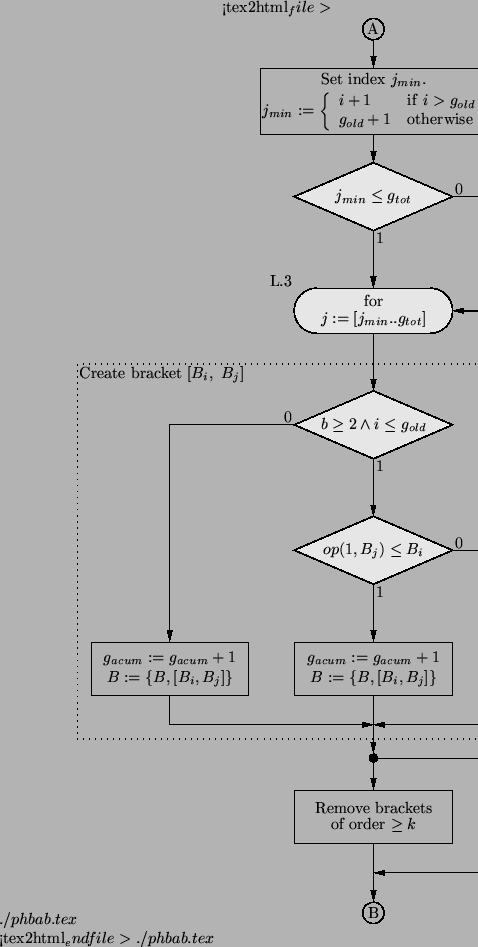 |
Figure 5:
Flow chart for the phb algorithm (contd. from
Fig. 4).
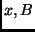 |




Next: phbize
Up: Function Reference
Previous: createLBobjects
Contents
Miguel Attilio Torres-Torriti
2004-05-31
![$[B_i,B_j]$](img495.png) '', shown in Fig.
'', shown in Fig.  ).
).
