Construct the differential equation for the logarithmic coordinates
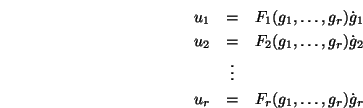 of the Wei-Norman formula, see wne, wner. of the Wei-Norman formula, see wne, wner.
|
Syntax e:=wnde(x,r,max_bracket_order,B,lbt);
Description
Constructs the differential equation for the logarithmic coordinates
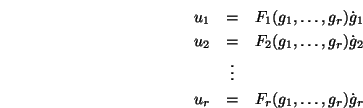 of the Wei-Norman formula. This function equates the
coefficients of the of the Wei-Norman formula. This function equates the
coefficients of the  in the left-hand
side of the Wei-Norman equation 40 to the corresponding
coefficients of in the left-hand
side of the Wei-Norman equation 40 to the corresponding
coefficients of  in the right-hand side 43,
yielding a set of equations of the form: in the right-hand side 43,
yielding a set of equations of the form:
or equivalently in matrix form as
where |
Arguments


max_bracket_order



Examples
The matrix wnde.
> eval(lc[1]);
[1 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ ]
[0 1 0 0 0 0 0 0 0 0 0 0 0 0]
[ ]
[0 g1~ 0 1 0 0 0 0 0 0 0 0 0 0]
[ ]
[ 2 ]
[0 1/2 g1~ 0 g1~ 0 0 0 0 0 0 0 0 0 0]
[ ]
[ 3 2 ]
[0 1/6 g1~ 0 1/2 g1~ 0 0 0 0 0 0 0 0 0 0]
[ ]
[0 0 1 0 0 0 0 0 0 0 0 0 0 0]
[ ]
[0 0 g1~ 0 0 0 0 0 0 0 0 0 0 0]
[ ]
[ 2 ]
[0 0 1/2 g1~ 0 0 0 0 0 0 0 0 0 0 0]
[ ]
[ 3 ]
[0 0 1/6 g1~ 0 0 0 0 0 0 0 0 0 0 0]
[ ]
[0 0 0 g3~ 0 0 0 0 0 0 0 0 0 0]
[ ]
[ 2 ]
[0 0 0 1/2 g3~ 0 0 0 0 0 0 0 0 0 0]
[ ]
[ ]
[0 0 0 g2~ 0 0 0 0 0 0 0 0 0 0]
[ ]
[ 2 ]
[0 0 0 1/2 g2~ 0 0 0 0 0 0 0 0 0 0]
[ ]
[0 0 0 g1~ g2~ 0 0 0 0 0 0 0 0 0 0]
Practical application examples involving the derivation of the
logarithmic coordinates for an underactuated rigid body in space can
be found in the directory ../ltp/dev, in the files
weinorman_rb1.ws and weinorman_rbfull.mws.
|
Notes
Care should be put when passing the P. Hall basis, the Lie bracket
table to this function, and the right-hand side of the Wei-Norman
equation. It could be the case that the number of brackets in each
argument are not consistent. This function attempts to construct the
list containing the actual basis for the Lie algebra from the P. Hall
basis and the Lie bracket table. It also tries to detect situation of
argument inconsistency, however the checking procedure is rather simple
still and it may not correctly identify all possible errors.
To avoid problems perhaps the best way is to provide the function with
the Lie algebra basis and pass it in the argument for the P. Hall
basis and pass an empty list or set as argument for the Lie bracket
table. The disadvantage of this approach is the possible calculation
involved in the determination of a suitable Lie algebra basis prior to
invoking wnde.
|
See Also
wne, wner.
|
References
| See [32] and references therein for an explanation on the derivation of the Wei-Norman equations. |