



Next: Function Reference
Up: Using LTP: Some Practical
Previous: Step 2: Calculation of
Contents
The aim here is to construct a finite dimensional realization of a nonlinear filter for the stochastic system described by (see [28,19]):
where 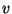 and
and 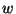 are independent Brownian motions. As suggested in [5] such a realization can be derived by applying Lie algebra techniques to the DMZ equation for the unnormalized conditional density
are independent Brownian motions. As suggested in [5] such a realization can be derived by applying Lie algebra techniques to the DMZ equation for the unnormalized conditional density 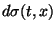 , given the observation process
, given the observation process
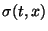 for system (29). The DMZ equation here is
for system (29). The DMZ equation here is
where the differential operators
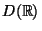 are defined by the following expressions on their common invariant domain
are defined by the following expressions on their common invariant domain 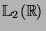 which is dense in
which is dense in
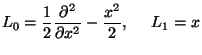 (see [28]):
(see [28]):
It will first be shown that the estimation Lie algebra
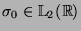 for the above problem is finite dimensional and solvable. Then, the solution of the Cauchy problem for any given
for the above problem is finite dimensional and solvable. Then, the solution of the Cauchy problem for any given
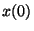 , representing the conditional density of
, representing the conditional density of 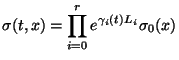 , can be written in the form of a product of exponentials, see [23]:
, can be written in the form of a product of exponentials, see [23]:
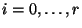 |
|
|
(30) |
where 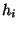 ,
, 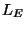 is a basis for the Lie algebra
is a basis for the Lie algebra 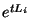 . The exponential
. The exponential 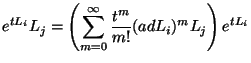 represents here a strongly continuous one-parameter semi-group operator defined on a Banach space
represents here a strongly continuous one-parameter semi-group operator defined on a Banach space
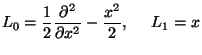 and corresponding to the infinitesimal generator
and corresponding to the infinitesimal generator 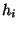 . The last representation is only valid if the Baker-Campbell-Hausdorff-Zassenhaus formula:
. The last representation is only valid if the Baker-Campbell-Hausdorff-Zassenhaus formula:
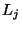 |
|
|
(31) |
holds for all the 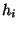 ,
, 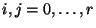 ,
,
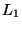 . As pointed out in [28] the validity of (31) is guaranteed if there exists a common, dense (in
. As pointed out in [28] the validity of (31) is guaranteed if there exists a common, dense (in
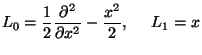 ), invariant under
), invariant under 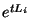 , set of analytic vectors for the estimation Lie algebra spanned by
, set of analytic vectors for the estimation Lie algebra spanned by 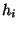 ,
, 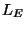 . Such a set can be constructed as the linear span of eigenvectors of the operator
. Such a set can be constructed as the linear span of eigenvectors of the operator 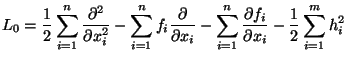 .
To check the solvability of
.
To check the solvability of 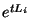 , the differential operators
, the differential operators 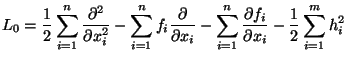 and
and 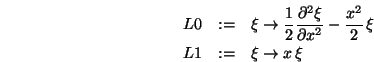 are first defined in Maple as follows:
are first defined in Maple as follows:
> L0:=xi->(1/2)*diff(xi,x$2)-(1/2)*x^2*xi;
L1:=xi->x*xi;
A basis for the Lie algebra of operators 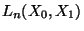 is obtained by considering a free nilpotent Lie algebra
is obtained by considering a free nilpotent Lie algebra 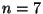 , where
, where  is a sufficiently high order and calculating its P. Hall basis. For example, for
is a sufficiently high order and calculating its P. Hall basis. For example, for 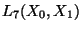 , the P. Hall basis for
, the P. Hall basis for 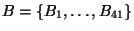 ,
,
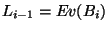 counts 41 elements and is constructed by invoking B:=phb(2,7). In this process, the package also delivers explicit bracket expressions for the basis elements in
counts 41 elements and is constructed by invoking B:=phb(2,7). In this process, the package also delivers explicit bracket expressions for the basis elements in 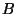 which are omitted here for reason of brevity. Identifying
which are omitted here for reason of brevity. Identifying
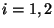 ,
, 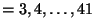 , the basis elements in
, the basis elements in 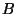 can thus be evaluated next by executing the LTP function calcLBdiffop(B[i],B[1..2],[L0,L1],[x]), for i
can thus be evaluated next by executing the LTP function calcLBdiffop(B[i],B[1..2],[L0,L1],[x]), for i
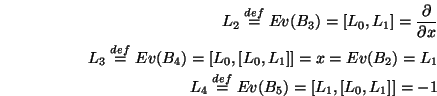 , yielding:
, yielding:
It can further be verified that the application of the evaluation map 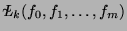 to the remaining brackets in the basis B reveals several linear dependencies between
to the remaining brackets in the basis B reveals several linear dependencies between
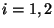 ,
, 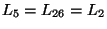 :
:
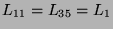 ,
,
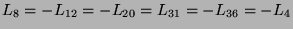 ,
,
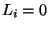 , and
, and 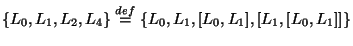 , for the remaining Lie products. From this calculation it follows that a basis for
, for the remaining Lie products. From this calculation it follows that a basis for 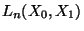 can be defined as
can be defined as
![$\{L_0,L_1,L_2,L_4\}\stackrel{def}{=}\{L_0,L_1,[L_0,L_1],[L_1,[L_0,L_1]]\}$](img443.png) . These calculations also show that the derived Lie algebra
. These calculations also show that the derived Lie algebra ![$[L_E,L_E]$](img444.png) is spanned by
is spanned by 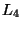 and
and 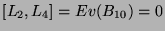 , and is nilpotent because
, and is nilpotent because
![$[L_2,L_4]=Ev(B_{10})=0$](img447.png) . Hence, the Lie algebra
. Hence, the Lie algebra 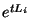 is solvable, by Corollary 5.3 in [36].
The representation (30) now becomes:
is solvable, by Corollary 5.3 in [36].
The representation (30) now becomes:
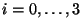 |
|
|
(32) |
is hence valid globally, see [45], and the functions 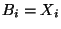 ,
, 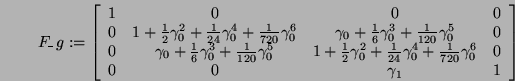 can be computed by quadrature of the Wei-Norman equations. The analytic expression for the Wei-Norman equations can be derived by executing the sequence of commands:
can be computed by quadrature of the Wei-Norman equations. The analytic expression for the Wei-Norman equations can be derived by executing the sequence of commands:
r:=4; # Basis dimension.
max_bracket_order:=6; # Degree of nilpotency minus one.
wn:=wner(r,max_bracke_order,BB,B,[SR]):
wnfe:=wnde(wn,r,{},BB,{}):
F_g:=eval(wnfe[1]):
The symbol [SR] is a Maple list containing the dependencies between the members of the basis 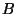 after application of the evaluation map
after application of the evaluation map 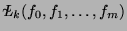 as derived above. The symbol
as derived above. The symbol F_g assumes value of the matrix 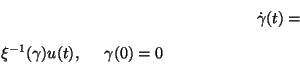 of equation (12) and is here:
of equation (12) and is here:
The entries 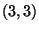 and
and 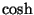 of F_g can be clearly be recognized as the first few terms in the Taylor series expansion for
of F_g can be clearly be recognized as the first few terms in the Taylor series expansion for 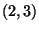 . Similarly, the entries
. Similarly, the entries 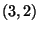 and
and 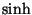 are recognized as the first few terms of the Taylor series for
are recognized as the first few terms of the Taylor series for 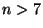 . Now, it can be verified that if the above calculations are repeated using a Hall basis of order
. Now, it can be verified that if the above calculations are repeated using a Hall basis of order 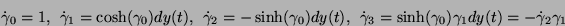 , then the entries of F_g will contain higher order terms of these Taylor series. Thus, by induction, it can be shown that these entries truly are the
, then the entries of F_g will contain higher order terms of these Taylor series. Thus, by induction, it can be shown that these entries truly are the 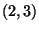 and
and 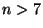 functions, so that the Wei-Norman equations for (32) in the form (14) are given by:
functions, so that the Wei-Norman equations for (32) in the form (14) are given by:
where
![$u=[1\ dy(t)\ 0\ 0]^T$](img459.png) .
The solution of these Wei-Norman equations constitutes the joint-sufficient statistics for the linear filtering problem of (29). Now, Mehler's formula (see [28]) allows to obtain the explicit expression for the one parameter semi-group
.
The solution of these Wei-Norman equations constitutes the joint-sufficient statistics for the linear filtering problem of (29). Now, Mehler's formula (see [28]) allows to obtain the explicit expression for the one parameter semi-group
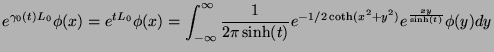 in the form of an integral operator as follows:
in the form of an integral operator as follows:
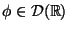 |
|
|
(33) |
for any
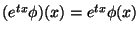 .
Since
.
Since
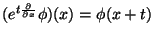 and
and
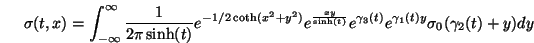 , then, finally, (32) and (33) combine into:
, then, finally, (32) and (33) combine into:
which is an explicit formula for the nonlinear filter for (29).




Next: Function Reference
Up: Using LTP: Some Practical
Previous: Step 2: Calculation of
Contents
Miguel Attilio Torres-Torriti
2004-05-31
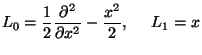 (see [28]):
(see [28]):
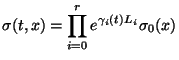 , can be written in the form of a product of exponentials, see [23]:
, can be written in the form of a product of exponentials, see [23]:
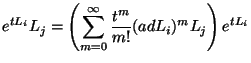 represents here a strongly continuous one-parameter semi-group operator defined on a Banach space
represents here a strongly continuous one-parameter semi-group operator defined on a Banach space
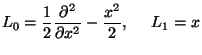 and corresponding to the infinitesimal generator
and corresponding to the infinitesimal generator 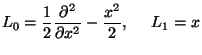 ), invariant under
), invariant under 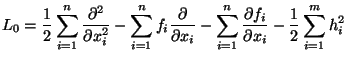 .
To check the solvability of
.
To check the solvability of 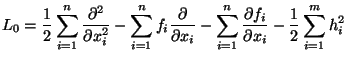 and
and 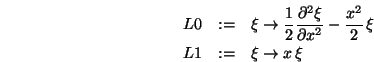 are first defined in Maple as follows:
are first defined in Maple as follows:
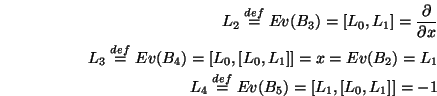 , yielding:
, yielding:
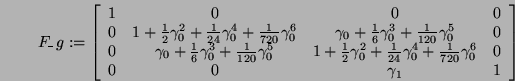 can be computed by quadrature of the Wei-Norman equations. The analytic expression for the Wei-Norman equations can be derived by executing the sequence of commands:
can be computed by quadrature of the Wei-Norman equations. The analytic expression for the Wei-Norman equations can be derived by executing the sequence of commands:
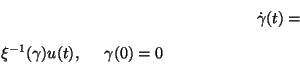 of equation (12) and is here:
of equation (12) and is here:
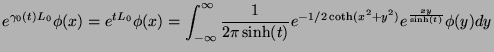 in the form of an integral operator as follows:
in the form of an integral operator as follows: