We consider the case of 2 unit speed agents searching the plane for a
single target. The agents can sense a region in the plane in a disk
about their position of radius, r. We will assume that both agents
adopt the same search strategy, so that without loss of generality, we
can perform analysis on the half-plane and a single agent
.
Following the advice of [4] we will adopt the appropriate model
of spiral search as the exploration strategy. In this circumstance,
spiral search simplifies to walking concentric circles of odd radius,
so that the boundary of the sensed regions just touch. This leaves a
measure zero set ( 
) of the plane
unsearched so that we are guaranteed to find the target if it lies
within the searched region. See figure 1 for a description
of the search pattern.
Figure 1: The path traced by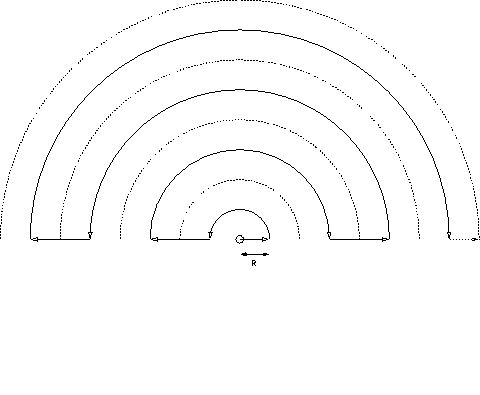 
of concentric hemi-circles.
The family of rendezvous strategies that we will consider can be
described as follows. Every time our agent arrives back at the border
of the half plane she has a choice to move back to the origin to meet
with the other agent, or continue to search the next level out of her
region. We will evaluate and analyze the cost of the alternate
behaviors and attempt to categorize the strategy family. Let us
describe the strategies in the following manner, let 
be
the strategy that rendezvous is attempted upon every i-th arrival at
the search boundary. Let 
be the positive integers then
rendezvous is attempted at border encounters from the set,
, for strategy 
. Define
to be the strategy of spiral search without rendezvous
attempts (since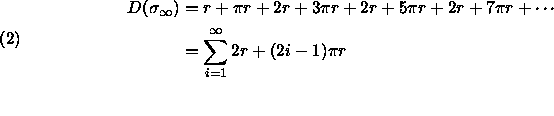 
). Consider the distance that is traversed during this
search,
In fact we can easily go ahead and categorize the distance traversed by each strategy in the family, by applying similar analysis. Note that the sum is chosen to reflect the distance traveled between rendezvous attempts, breaking the infinite sum in this way will be useful when analyzing the strategies according to rendezvous attempts and we can safely take the sum term-wise due to the compactness of the plane. Yielding the sequence,
taking the sum, of course as 
. But splitting the sums
up in this fashion allows us to see the pattern that evolves by the
members on each of the respective rendezvous attempts. The pattern
that evolves is intuitive enough since for each member the distance
traveled between rendezvous iterations consecutive odd traversals of
hemi-circles, followed by the trip to the origin. This accounts for
the terms in (4), the 
term for the exploration
trips, and the r term accounting for the rendezvous trips.
Now we can characterize the distance that is wasted,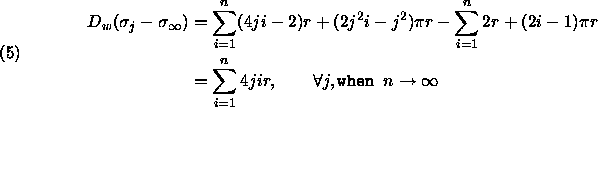 
, performing
rendezvous by taking the difference of (4) and
(2) resulting in the extra distance traveled at each
iteration.
How then does this figure into our performance scheme (1)? If
this is the accumulated distance that we waste at each iteration then
our opportunity cost is searching this far into the next level of the
exploration. So what is our expected gain from further search? It is
the area, A, that we will see on the next iteration of the search
strategy. This is easy enough to figure out, we have already seen
this as the area, , term in (4).
Then from (1) we see that what we expect to gain is area of the
next iteration of search for our strategy, 
. This is in
inverse proportion to the accumulated distance that we have walked for
rendezvous purposes. That proportion is what we need to understand.
Figure: The Quantitative Performance (1) of
exploration versus rendezvous overhead
The function is plotted in figure 2 and is seen to have
quadratic cost in terms of the strategy chosen. It makes sense to
have strategies of j<1, which would correspond to not exploring the
entire semi-circle before returning to the rendezvous origin, perhaps
in circumstance where the sensing region was very large relative to
the speed moved, 
.
