[Prev (Using the Logic Modules)][Next (Reverb and Echo Effects)][Table of Contents]
Chapter 10. Algorithmic Composition
Most of the readers of this document will no doubt be familiar with
creating music using sequencing software or hardware. In this compositional
process the composer determines the melody and the rhythm and transfers
them to the sequencer by hand. But wouldn't it be nice if the computer
could do some of the composing work? Is it even possible for a computer
to do so? The computer generation of music is often referred to as
algorithmic composition where the word algorithmic refers to the
use of a computer program, or algorithm, to specify the music structures.
The Nord Modular contains some modules that are useful for composition.
Some of these, such as the Sequencer modules, require human interaction to
define the notes and rhythms. Others, such as the pattern generators, can
run on their own. There are many Nord Modular patches in the archives,
often referred to as "noodles", which need no human interaction to produce
interesting music. Most of these noodles are carefully hand-crafted, however,
and the music is clearly man-made. The noodles are often of a fixed
nature, and cannot generate radically different musical creations.
But, in spite of this, the Nord Modular IS capable of pure algorithmic
composition, which can generate radically different music with little
human intervention beyond setting a few parameters. In this chapter we
will look at a few different types of algorithmic composition that can
be implemented on the Nord Modular.
10.1 Chaos and Fractal Music
Mathematic chaos is a study of rather simple systems that produce
rather complicated behaviour. This is perfect for making music on
modular synthesizers, since we all know interesting music is complicated,
but we can't implement very complicated equations with the limited
resources of modular synths.
The patterns produced by chaotic systems bear some similarities to
random noise, such as we use to make snare drums and so forth, but
tend to have much more structure. The chaotic patterns tend to be
"quasi-periodic", that is, the output of the system follows a regular
pattern, but not exaclty. From cycle to cycle, the patterns are slightly
different. Obviously, totally random noise is not too useful for
specifying melodies and rhythms (although some may argue to the contrary).
But chaotic patterns seem to have just the right mix of randomness
and repeatability to produce interesting music. In the following section
we present two Nord Modular patches which use different chaotic
systems to produce self-generated music.
The first patch we will look at was designed by Rob Hordijk. It
implements four simple non-linear ecosystems, defined by the
formula that Mitchell Feigenbaum used to come to his
'Chaos'-theory. The equation that governs this chaotic system is
X(t+1) = G * X(t) * (1 - X(t))
This equation is known as the Logistic Equation.
It was first used to model the population of animal species from
year to year. In the equation above X(t)
is the ratio of the actual population to the maximum population.
Each iteration (e.g. from one year to the next)
gives the new relative population in terms of the old one.
The parameter G is the effective growth rate.
The two terms in the
equations model the fact that more animals will have more offspring
(so growth is proportional to X), but will compete for resources (so
that growth is also proportional to (1-X)).
As the population increases the load on the environment increases
reducing the availability of resources and limiting the growth rate.
This is modeled by the (1-X(t)) term.
For growth rates G less than 1, X(t) tends to 0.
For growth rates between 1 and 3, X(t) tends to 1 - 1/G. Beyond G=3
a bifurcation occurs causing an oscillation from year to year.
(corresponding to high and low populations in alternate years).
Further bifurcations occur until at G = 3.53... chaotic dynamics set in.
For values of G greater than 4 the system diverges (goes off to
-infinity, or saturates at the most negative possible value).
What does all this animal husbandry have to do with the dog-eat-dog
world of musical synthesis? Well, the chaotic behaviour exhibited by
the logistic function can be used to produce interesting music.
In the patch below the X values are used to play notes,
but they could be used to control anything.
In the patch there are four separate chaotic systems implemented.
The systems can
influence each other. They can be helped by their right neighbours to
become more alive while their growth can be suppressed by their left
neighbours. Sounds like real life, don't it? Well, actually it sounds like
the Nord Modular, so don't worry, no need for peace keeping forces in your machine.
Some settings can make all four systems slowly succumb, others
can result in chaotic behaviour, and somewhere in between there should be
"easy livin'". In figure 10.1 we show the behaviour of the logistic
equation for various settings of the G parameter.
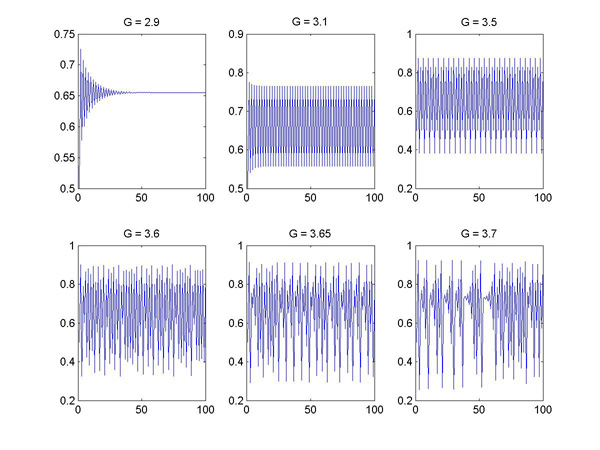
Figure 10.1. The behaviour of the logistic equation for various
settings of the G parameter. For G less than 3, the system quickly
settles to a fixed value. For G between 3 and 3.53 oscillations occur. For
G greater than 3.53 chaotic dynamics result.
In the figure below we show 1/4 of the entire patch, corresponding to
one of the four chaotic systems (clicking on the figure will give the
entire patch, however).
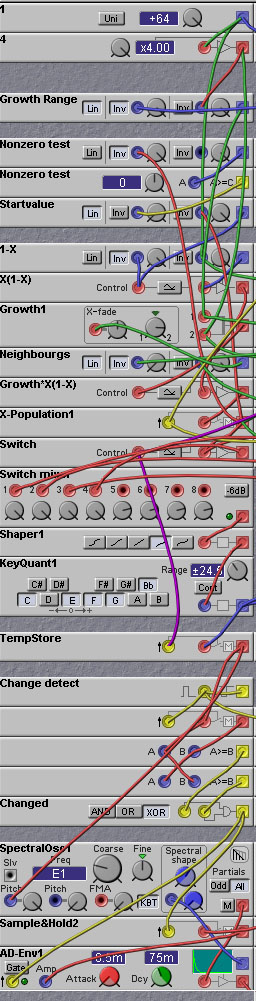
Figure 10.2. Chaotic system patch using the Feigenbaum attractor
(R. Hordijk).
For the equation to work it can not start with a zero value for X, as
nothing can grow out of nothing unless some "Act of God" is involved. So a
provision is made that a small value is automatically added to X, only in
the first cycle when X is zero due to patch loading conditions.
The following patch implements another type of Chaotic system, this
one termed the Henon strange attractor.
This system was discovered by the French astronomer Michel Henon while
studying the dynamics of stars moving within galaxies.
The equations for this system are:
x(n+1) = 1 + y(n) - a*x(n)*x(n)
y(n+1) = b*x(n)
The Henon system is 2-dimensional, unlike the logistic system described
earlier, which was 1-dimensional. That means it produces two values which
you can use to control various aspects of the music. As with the
logistic equation, certain settings of the parameters a and b give
rise to chaotic behaviour. An example is shown in figure 10.3, which
plots the values of x and y for a setting of a=1.4, b=0.3. Notice that
the points are distributed along a smooth curve, so that overall
pattern of the values of x and y is appears non-random, and
repeatable. At any given time, however, the values are essentially
randomly distributed along this curve. Thus we have a "structured
randomness", just the thing we are looking for in algorithmic music!
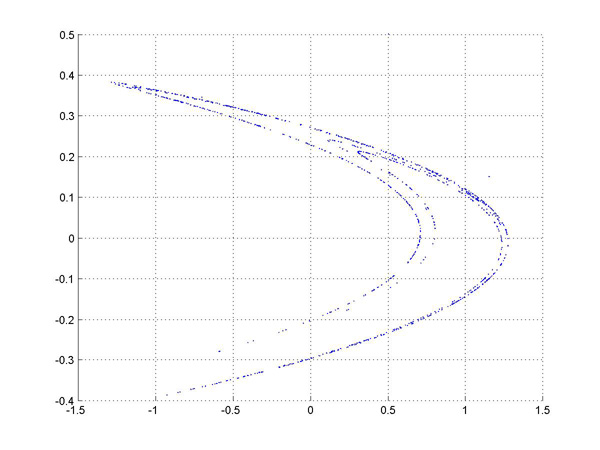
Figure 10.3. Behaviour of the Henon attractor for a setting of
a=1.4, b=0.3.
The following
patch uses the Henon equations to generate a quasi-periodic melody
(in Eb major, but you can change
this by changing the notes selected in the key quantizers).
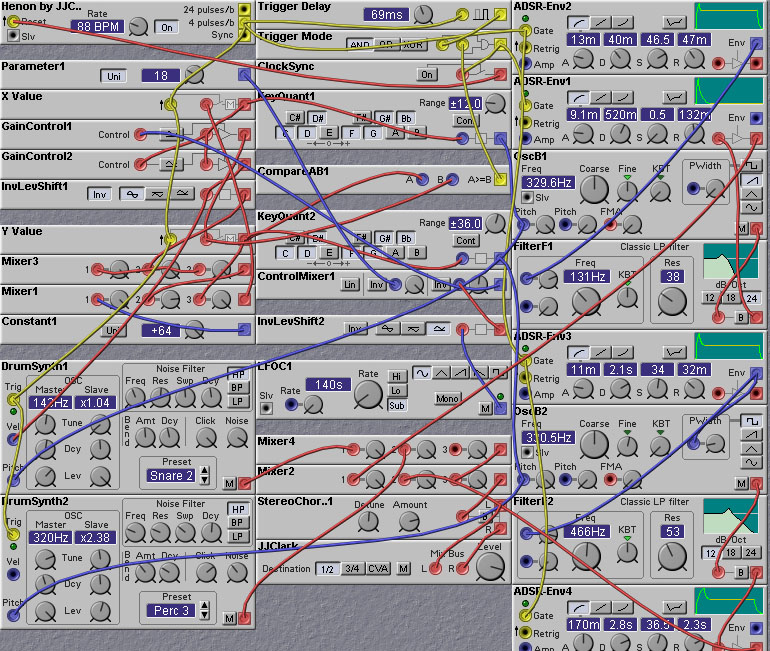
Figure 10.4. A chaotic noodle patch using the Henon strange
attractor to vary the pitches and rhythms (J. Clark).
Knob 1 controls the dynamics, and determines whether
the pattern is repetitive or chaotic.
Knob 2 controls the level of a LFO that adjusts the attractor parameter
(Knob 1) to provide a constantly (slowly changing) dynamic. Turn knob 2
to zero to maintain a steady attractor type.
Knob 3 sets the tempo.
Knob 4 sets the delay in the triggering of the second voice.
Knob 5 is used to turn on or off the syncing of the master clock
with the second voice trigger. Turning this on causes a change in
the beat pattern.
Knob 6 is used to select one of three different modes for
generating the second voice trigger.
You can try to play along with the pattern with your
piano instead of doing all those tedious Hanon piano exercises!
There is a wealth of information on Chaos on the web and in the
libraries. A good starting point would be to read the very accessible
book "Chaos: making a new science" from James Gleick. It's a good
introduction into chaotic behaviour.
The chaotic systems that we have talked about so far are of a class
known as iterative systems, in which an operation is repeatedly
applied in discrete times. One can also obtain chaotic behavior in
continuous dynamical systems. These are much harder to analyze
mathematically, but they are just as easy to use. While there is a
great variety of dynamical systems that exhibit chaos, from the point
of view of modular music synthesis one of the most useful is the
coupling of three voltage controlled oscillators, connected in a
ring. The idea is to have oscillator 1 frequency modulate oscillator
2, oscillator 2 frequency modulate oscillator 3, and oscillator 3
being fed back to frequency modulate oscillator 1. Depending on the
modulation amount settings, such a circuit produces chaotic outputs for
each of the oscillators. This approach can be used for audio-rate
oscillators as well as for LFOs. The audio-rate circuit produces
sounds that sound like (rather sickly) noise, which may be useful for
some percussive sounds or simulating broken steam radiators. For
algorithmic synthesis, however, chaotic LFO chains are much more
useful. The outputs of the LFOs can be used to control sound
parameters (pitch, filter cutoff, amplitude, etc) or to trigger
events. An example is shown in the following patch:
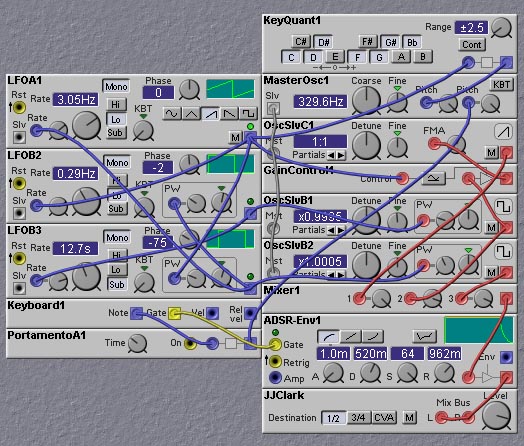
Figure 10.5. A chaotic noodle patch using 3 coupled LFOs (J. Clark).
In this patch the outputs of the LFOs are used to control (through a
note quantizer) the note pitches, the pulse-widths of 2 audio
oscillators, and the FM amount for one audio oscillator. Thus the
pitch seems to warble in a quasi-random fashion, as does the timbre of
the notes (due to the time-varying PWM and FM).
10.3 Cellular Automata
Cellular automata are instances of Finite State Machines, where the
state of the system is represented as binary values in a set of
cells. The cell values are updated regularly based on the values in
neighboring cells, according to some rule. Perhaps the most famous
example of a cellular automaton is that used in the "game of life",
devised by Princeton mathematician John Conway.
In a "game of life" cellular automaton each cell carries a binary (0
or 1) value. If the value is 0 the cell is said to be "dead",
otherwise if its value is "1", the cell is said to be "alive". Updates
of cell values are based on the number of "living" neighbors. A
typical rule for the updating process is to set a cell to the "alive"
state is the number of living neighbors is less than a certain high
threshold (not too crowded) and greater than a certain low threshold
(not too lonely). Otherwise the cell is set to the "dead"
state. For certain choices of the thresholds and initial population
patterns, dynamic and persistent behaviour can arise in the state
values of the overall cellular automata.
An example of the evolution of a simple 1-dimensional cellular automaton
is shown in figure 10.5. The behaviour of the automata is set by
a rule which maps the local state (the value of a cell and those of its
neighbors) into a new state value. The rule can be described in a
look-up table that gives a value of either 0 or 1 for every possible
combination of neighborhood cell values. The automaton shown in figure
10.5 has 2 neighbors for each cell.
The complexity that can be obtained from such
simple rules is clearly evident.

Figure 10.6. An example of the patterns generated by
a 1-dimensional cellular automaton. The
vertical dimension represents time and the horizontal dimension
corresponds to the location of the cells. There are 2-neighbors for each
cell.
If we implement a cellular automata in the Nord Modular we can use
cell state values to control various parameters and generate
interesting (?) music. The following patch illustrates the implementation
of a simple Cellular Automaton. It implements a 1-D array, with each cell
have 2 neighbors. A "Life" type of rule is used, where a cell state is
set to one if there is only one active cell in its neighborhood (which
includes itself). This is basically the same rule that was used to generate
the pattern shown in figure 10.5.
The cell state is stored in a Sample-Hold module and
cells are updated whenever the Sample-Hold modules are clocked.
The update values are computed by the logic gates attached to the S/H
outputs. In this case the logic merely determines when there is exactly one
logically high output in a neighborhood of three S/H outputs. The
patch implements 6 cells, connected in a circular ring. The outputs of
each cell are used to trigger an envelope generator. Of course, you could
use these outputs for anything. I used them to trigger the envelope generators
since the gate LEDs on the envelope generators gives a visual indication of
the cellular automata states. The keyboard gate is used to briefly set one
of the cells states to one. For the particular rule that is used, the
cellular automaton will go through 4 active states and then stick and hold
on the "all-zeroes" state. By changing the logic circuits that are used
to update the state you can get different patterns.
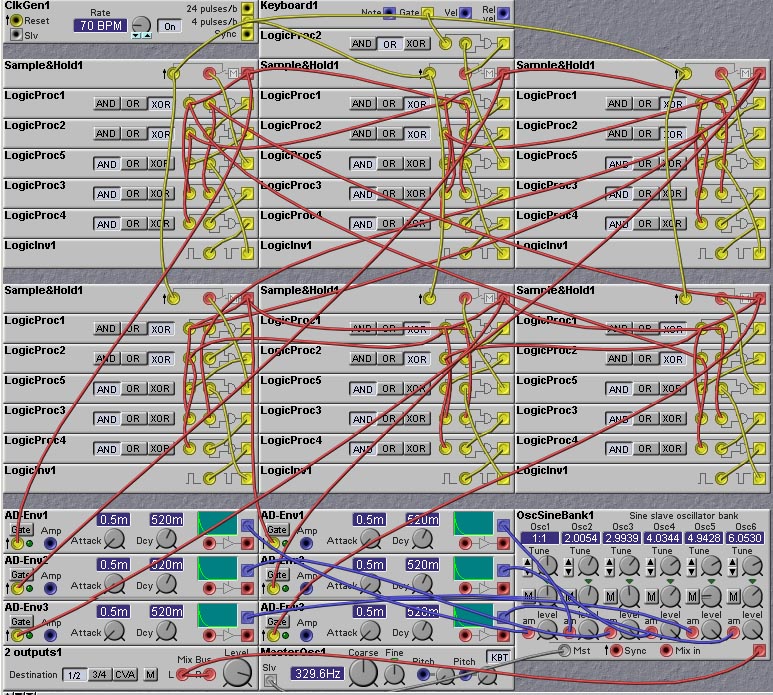
Figure 10.7. A simple 1-D cellular automata patch for the Nord Modular
(J. Clark).
The cellular automata patch shown above uses logic gates to implement the
state updating. This approach is rather inflexible, as changing the update
rule requires changing the logic circuitry. Thus, one can't change rules on
the fly, as it were. In most software implementations of cellular automata
the updating is done via a look-up table, wherein the neighborhood state is
used to index a look-up table memory which stores the appropriate update
value. Changing the update procedure simply requires changing the values
in the look-up table memory, something which could be done on the fly.
Unfortunately, the Nord Modular does not contain any random-access,
re-programmable memory modules that could be used for a look-up table.
One could cobble together something out of sample-hold modules, but it
would be very cumbersome. So, what to do? How can we make a programmable
cellular automaton on the Nord Modular?
Well, the always resourceful Rob
Hordijk came up with a solution, which uses the knobs on the
front panel of the Nord Modular as the programmable lookup table!
His implementation is shown in the following figure. It doesn't
immediately look like a cellular automaton, as the neighborhood
structure is hidden away, but the overall behaviour is that of a cellular
automaton.

Figure 10.8. A cellular automata patch for the Nord Modular (R. Hordijk).
In this patch,
four-bit 'nibbles', implicitly representing a neighborhood state,
are used to address sixteen memory locations.
These locations themselves each hold a nibble, which represent the
updated neighborhood values. These locations are examined (looked up)
on every clockpulse, to be used as the address in the next
iteration. There are three usable nibbles in this patch, each with the same
set of 'rules', that is they share the same lookup memory locations. The
contents of the sixteen memory locations are in practise the sixteen
knob values.
The 'nibbles' are conveniently stored in S&H
modules. The nibbles are decoded using one-of-sixteen circuits (the group of
compare and XOR modules) and used to address one of the sixteen knobs.
Each knob delivers
a new 'nibble' to store in the S&H on the next clockpulse. Also the sixteen
outputs of the one-of-sixteen circuit are coded back to the real four bits
of a nibble, using so called 'mickey mouse'-logic (the four eight-input
mixers). We now have three types of output to work with, (1) the sixteen
separate logic outputs of the XOR-modules, only one of these can be on, (2)
the three S&H's that can have sixteen values between 0 and 64, in
steps of 4, and (3) the four discrete bits that form the
'nibble' at the outputs of the eight-input mixers, whose values must be
interpreted as 0 or anything greater than 0.
What to do with the output values is up to you. The patch shown above
uses the outputs to trigger envelope generators attached to sine wave
oscillators of various frequencies, thereby producing different
melodies.
To program a pattern in this patch follow these rules:
If knob1 is closed the next selected knob will be knob1 again. If knob1
points to knob2, that one will be the next knob and if that one points to
knob5, which on it's turn points to knob1, the pattern will be knob1 ->
knob2 -> knob5 -> knob1 -> knob2 -> knob5 -> knob1, etc. So here repetition
occurs after three clockpulses, but in general the longest pattern will be
sixteen clocks. So to make it more interesting knob16 is replaced by a
randomvalue. If in a pattern knob16 is reached it jumps randomly to one of
the other knobs. Now it starts to get interesting as in the example the
patterns would never use knob3 and knob4 and all knobs after knob5. But if
knob3 points to knob4 and knob4 points to knob16, and we will also let
knob5 point to knob16 instead of knob1, and all other knobs point to either
knob1 or knob 3, the pattern goes random, but not completely random, it
starts to randomly play the small fragments all ending with knob16,
sometimes preceded by a randomly chosen knob and sometimes jumping into the
middle of the first two fragments. There is one 'disallowed' state in the
knobsettings, if a knob points to itself the pattern 'hangs' on that knob
-> the 'population' sadly dies and it's game over.
On loading the patch in a NM slot, the S&H modules will be initialised with
values of zero, so the three nibbles all point to knob1. But for every
nibble, when knob16 is reached a different random value for each nibble is
generated, so the combination of the three nibbles gives a more varied
pattern than only one nibble, but still fragments will be more or less
recognizable according to the knobsettings.
So knob16 can actually be deassigned in this particular patch, as tweaking
it doesn't do anything since it is replaced by a random value.
The 'rule'-values or 'to what value should a knob be set to make it jump to
which other one' are:
Jump to Knob1: 0-7
Jump to Knob2: 8-15
Jump to Knob3: 16-23
Jump to Knob4: 24-31
Jump to Knob5: 32-39
Jump to Knob6: 40-47
Jump to Knob7: 48-55
Jump to Knob8: 56-63
Jump to Knob9: 64-71
Jump to Knob10: 72-79
Jump to Knob11: 80-87
Jump to Knob12: 88-95
Jump to Knob13: 96-103
Jump to Knob14: 104-111
Jump to Knob15: 112-119
Jump to Knob16: 120-127
One of the favorite pastimes of Nord Modular programmers is the
"cooking of noodles". Noodles refer to self-running patches that have
some (hopefully interesting) temporal variation in the sound. Some
noodles are melodic, some are extended "drones", where the variation
is timbral in nature, and some are just plain wierd.
In this section I will try to give some tips for creating your own
noodles, but these should only be considered as examples, and
shouldn't limit your own creative explorations!.
First off, you should decide what sort of noodle you want to create.
That is, do you want a melodic noodle? Do you want a rythmic noodle?
Do you want a timbral noodle? A combination of these? None of the
above? This will tell you what type of parameters will be
time-varying. Time-variation is the key in cooking noodles. As Jan
Punter, one of the master noodle chefs for the Nord Modular, says,
noodle makers should concentrate on the "blue wires" in the Nord
Modular patch. That is, the control structures are paramount. The
actual sound generation is less important, although of course you do want to
have interesting sounds for the most part.
You will need to have some mechanism(s) for producing the temporal
variations in the control signals. The most basic ways of doing this
are to use LFOs, Sample-Hold modules sampling noise, the Sequencer
modules, and the Random generators. By themselves, these modules give
uninteresting noodles, as they are either too static (e.g. with the
sequencer or LFO modules) or too random (e.g. with the random
generators or with sample-hold noise). Such noodles sound stereotyped
and trite. Rise above the masses! More interesting variation can be
obtained using the chaotic control signal generation techniques
described earlier in this chapter.
Some slow variation is possible by working with the audio-chain as
well. Feedback, as we have seen in the case of three coupled
oscillators, can give rise to chaotic behavior. This is not limited to
feedback to frequency modulation inputs, however. Chaotic and
unpredictable behaviour can result from all sorts of feedback, whether
it be amplitude modulation feedback, filter cutoff modulation,
etc. Especially good for creating unpredictable havoc are the delay
module (inserted into feedback paths or use feedback to control delay
times) and feedback of audio signals to sync inputs on
oscillators. These provide very interesting timbral variations that
seem to occur in bursts.
Another useful technique is to use crossfade modules to dynamically
select different control signals or audio pathways. The crossfade
modules themselves can be controlled by chaotic or semi-periodic
signals to give noodles that are locally quite well-behaved but from
time-to-time change character abruptly. Logic circuits can be used to
control the crossfaders as well, for example using counters,
flip-flops or even event sequencers, to control the evolution of the
noodle. Sample-Hold modules can be used to "freeze" certain control
signals for a time.
Experiment with every module and with every type of parameter. For
example, I find that using the AHD and MOD envelope modules can be
very effective in noodling, since they have modulatable timing
parameters. The digitizer module also finds its way into many noodles.
Noodle cookers should have an aversion to leaving any input
unconnected. An unconnected input is a wasted opportunity for
interesting variation!
Most good noodles have a certain "feel" to them. Some are jazzy, some
bluesy, and others have a middle-eastern feel. You need to keep tight
control over such noodles, to ensure that they don't stray from their
intended groove. To do this, use mixers and attenuators to keep levels
in a certain range, and employ quantizers. Note quantizers can be used
to impose scales (e.g. the blues scale) on a noodle. Digitizer modules
can be used to limit the range of control signal levels. The
following patch shows a noodle that has a definite feel to it, that of
an aging 70's prog-rocker aimlessly noodling away on his synth. This
patch is an expansion of the patch shown in figure 10.5. A chain of 3
coupled LFOs is used to generate three chaotic control signals, which
are used to control the pitch and timbre of the notes. One of the
chaotic control signals is used to trigger the amplitude envelope,
thereby impose a quasi-random rythm. The 70's synth feel is created
through the use of portamento and resonant filtering, as well as by
the imposition of a minor scale through use of a note quantizer.
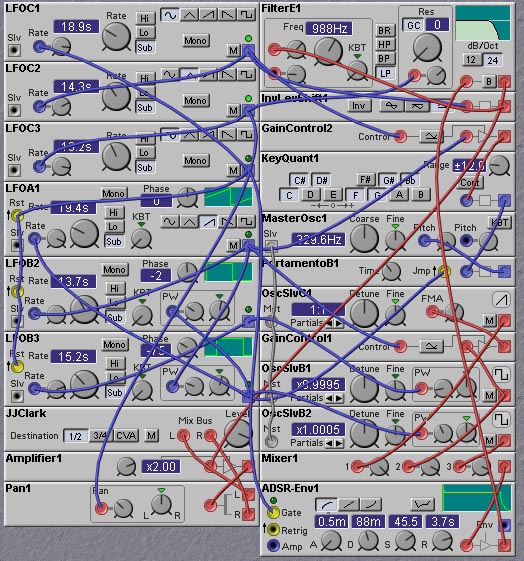
Figure 10.9. A chaotic noodle patch using 3 coupled LFOs. The
sound is designed to give the feel of a 70's prog-rocker aimlessly noodling away
on his synth keyboard (J. Clark).
One of my most frequently employed methods for getting interesting
noodles is to take somebody else's posted noodle patch and "mod" it
(modify, hack, deconstruct,...) to yield something completely
different (yes, I know, I am lazy). I usually do this by re-wiring
some of the control signals, changing some of the parameters
(e.g. cutoff frequencies, osc frequencies, etc), adding in osc sync,
and inserting feedback paths. If there are sequencer modules in the
original patch their settings should be altered (e.g. melodies and
rhythms changed). An example of this is shown in the following
patch, which is a mod of K. Lex. Pattyrson's patch
KrypixMia.pch. K. Lex (who
goes by many on-line aliases) is one of the masters of noodle
programming, and it is worth the time to download his patches and give
them a listen.
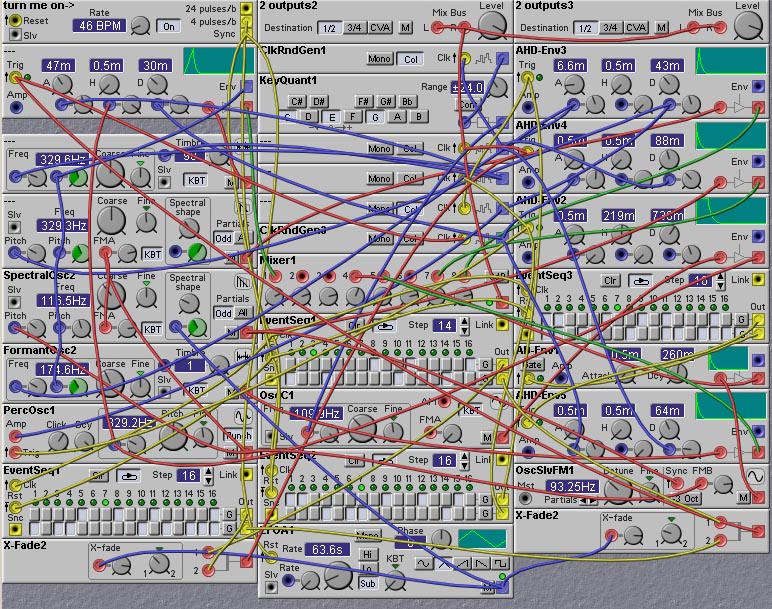
Figure 10.10. A sonically complex noodle patch
adapted from another noodle patch (J. Clark from L. Pattyrson).
You can see by the mess of wires in this patch that noodles can be
quite complex. In fact this noodle patch is one of the simpler ones
out there. Most are even more complex. Even so, the best way to learn
how to create your own noodles is to look at other people's noodle and
see how they do it. Because of their complexity it can be difficult to
understand what is going on. You should try to focus on the control
signal structure and see what is modulating what. Also look for
feedback, as this can also significantly affect the temporal
variations. The sound generation chain itself is not so important from
the perspective of the noodle maker.
[Prev (Using the Logic Modules)][Next (Reverb and Echo Effects)][Table of Contents]

(c) James Clark 2003










