← Return to All Projects
Area and Length Minimizing Flows for Shape Segmentation
Area and Length Minimizing Flows for
Shape Segmentation
A number of different active contour models have been proposed which unify the curve
evolution framework with classical energy minimization techniques for
segmentation, such as snakes. The essential idea is to evolve a curve (in 2D)
or a surface (in 3D) under constraints from image forces so that it clings to
features of interest in an intensity image. Recently the evolution equation
has been derived from first principles as the gradient flow that minimizes a
modified length functional, tailored to features such as edges. However,
because the flow may be slow to converge in practice, a constant (hyperbolic)
term is added to keep the curve/surface moving in the desired direction. In
our work, we have derive a modification of this term based on the gradient flow
derived from a weighted area functional, with image dependent weighting
factor. When combined with an earlier modified length gradient flow in the
literature we obtain a pde which offers a number of advantages, as illustrated by several
examples of shape segmentation on medical images. In many cases the weighted
area flow may be used on its own, with significant computational savings.

Figure 1. The boundaries of a
cat are captured after 300 iterations.
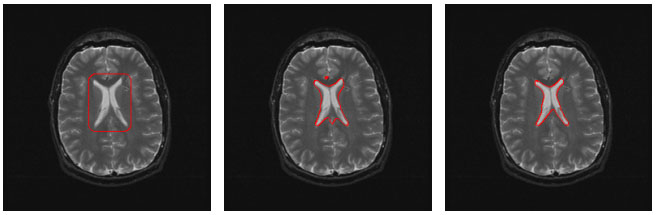
Figure 2. The ventricles of an MR image
of the human brain are captured by a geometric flow.
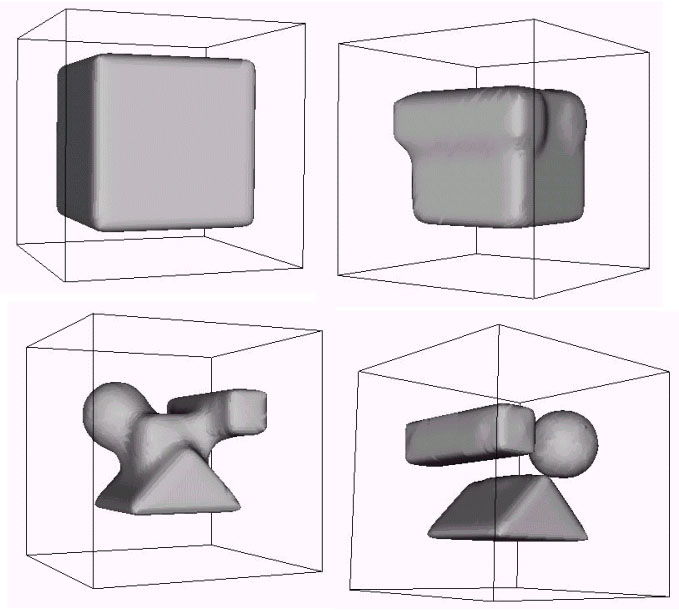
Figure 3. A cube evolves towards
3 synthetic objects.
-
- 1
-
K. Siddiqi, Y. B. Lauziere, A. Tannenbaum and S. W. Zucker.
Area and Length Minimizing Flows for Shape Segmentation.
IEEE Transactions on Image Processing, 7:3, pp. 433-443, 1998.
- 2
-
R. Malladi, J. A. Sethian and B. C. Vemuri.
Shape modeling with front propagation: A level set approach.
IEEE Transactions On Pattern Analysis and Machine Intelligence, 17:2, pp.158-175, 1995.
- 3
-
S. Kichenassamy, A. Kumar, P. Olver, A. Tannenbaum and A. Yezzi.
Conformal curvature flows: From phase transitions to active vision.
Archives of Rational Mechanics and Analysis, 134:275-301, 1996.
- 4
-
V. Caselles, R. Kimmel and G. Sapiro.
Geodesic active contours.
In ICCV'1995, 694-699, 1995.
Last update: November, 2003.
