Shape Analysis Group
Blood Vessel Analysis
Maxime Descoteaux
Introduction
Problem
Approach
References
Examples
Introduction
A three-dimensional (3D) representation of vasculature in the brain is extremely important in image-guided neurosurgery, pre-operation planning and clinical analysis. Typically, the data is available in a set of two-dimensional slices covering the brain, where a lot of information is present but noisy and hidden in between slices. Experts have to select and color the desired regions of slices before a program connects the colored components. This is tedious, not precise and prone to human error. There is no reason why one could not obtain improved results using intelligent shape models and automatic reconstruction algorithms. In the course of my master's research, I have mastered the theory of such model-based techniques using invariant geometric flows for blood vessel segmentation. These types of evolution equations are flexible and adaptable to new constraints and external forces. The essential idea is to evolve a surface in 3D so that it clings to the features of interest in the image.
Problem
We are given a magnetic resonance sequence of images (MRI) like the proton density shown below. Note that blood vessels appear dark on bright structures in PD images.
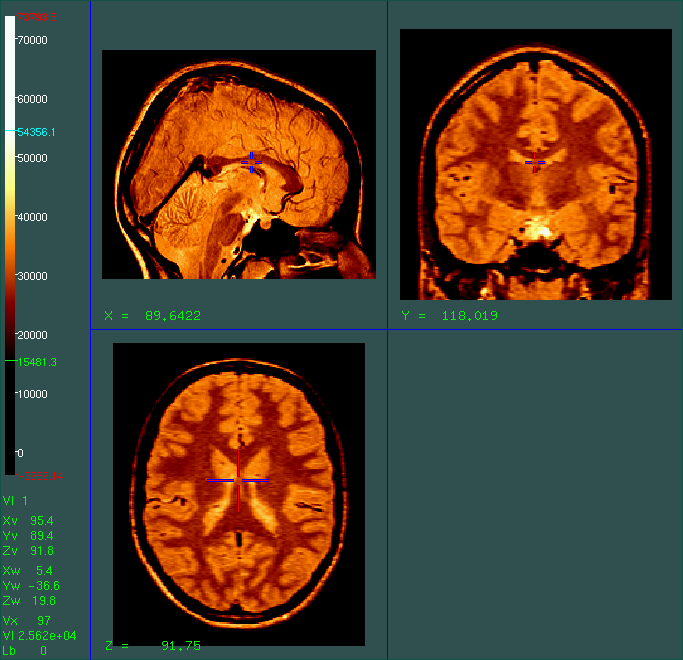
Currently, most blood vessel segmentation approaches in the literature
work on specific MRA (Magnetic Resonance Angiogram) examples but are
not applicable on common MRI sequences like PD, T1 or T2.
The challenge is to detect and segment the 3D vasculature tree
present in that kind of standard MR image commonly used in all hospitals.
Approach
We use the Hessian matrix to locally describe the structure of the image. Frangi et al. [2] defined a multiscale vesselness measure based on eigen values of the Hessian matrix. The operator is designed to be maximum at the vessel's centerline. A voxel belonging to a voxel region will ideally have its smallest eigen value very close to zero and the other two of large magnitude and almost equal. Finally, the eigen vector corresponding to the smallest eigen value gives the vessel's orientation. Examples are shown below. Here we visualize a level set of the maximum vesselness measure, with the eigen vector overlayed.
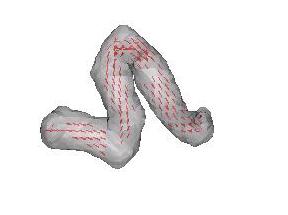
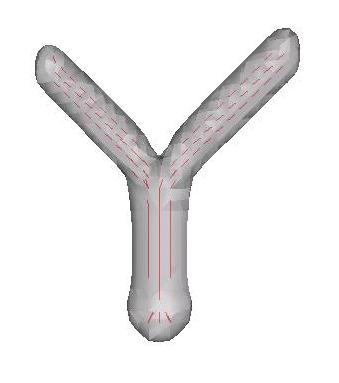
Figure 1. Synthetic branching and helix example
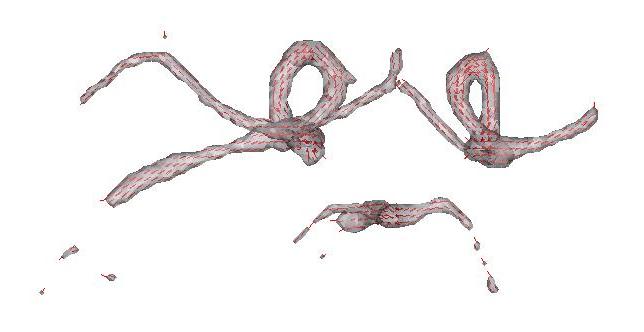
Figure 2. Cropped region of a MRA
We see that the eigen vector agrees nicely with the vessel orientation. Hence, at every voxel, we have a vesselness measure. Moreover, for strong vesselness quantities we also have the vessel's orientation and the vessel's radius (scale at which the maximum vesselness was detected).
Now, we have enough information to drive a flow that will cling to blood vessels. We are working on an augmentation of the flux maximizing geometric flow created by Vasilevskiy and Siddiqi in [2]. Their flow evolves a surface in a 3D vector field so as to increase the inward flux through its boundary as fast as possible. The gradient flow for this is
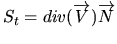
The evolution is simple and has an elegant interpretation. However, it does not include any geometrical properties of the vessels to be segmented.
We are investigating the augmentation of this method by incorporating information about the geometry of tube-like structures. As seen before, the multiscale eigen value and eigen vector analysis of the Hessian matrix provides information on the location, direction and size of vessels. The key idea is to locally fit and align ellipsoids (such as those seen in Figure 3) close to the true vessel boundary, which allows the computation of a flux map which takes into account the implied scale at which a vessel occurs. Thus the evolution has a model-based component and can be applied to a richer class of images than most geometric flows proposed for recovering tubular structures.

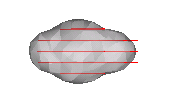
Figure 3. Ellipsoid of a given orientation and a scale to fit the true vessel boundaries.
Examples
Here is the result of the flux maximizing flow segmentation on a MRA image presented in [1]. A flow version of the augmentation that considers the estimated vessel geometry of tube-like structures will be available soon.
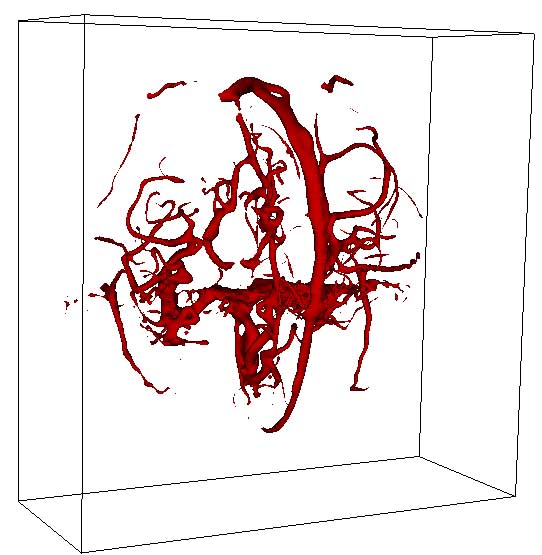
Key References
- 1
-
A. Vasilevskiy and K. Siddiqi
Flux maximizing geometric flows.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 24:12, pp. 1-14, 2002. - 2
-
A. Frangi, W. Niessen, K.L. Vincken, and M.A. Viergever
Multiscale vessel enhancement filtering.
Proc. MICCAI'98, pp.130-137, 1998. - 3
-
K. Krissian, G. Malandain, N. Ayache
Model-based detection of tubular structures in 3D images.
Computer Vision and Image Understanding, 80:2, pp. 130-171, Nov. 2000.