Diffusion Imaging and Fibre Tractography


My research involves both acquisition of magnetic resonance imaging (MRI) data and post-processing techniques. Specifically, I am working on an MRI modality called diffusion imaging and use computer vision techniques to infer white matter fibre connectivity in the central nervous system (CNS) from the base MRI images. Diffusion imaging is a method for measuring the displacement distribution of water molecules in vivo. From the displacement distribution, we can infer the fibre orientation or orientations in each imaging volume element (or voxel). With suitable post-processing techniuqes, we can reconstruct 3D white matter fibre bundles from these displacement distributions, along with the uncertainty associated with these connections. Below is a pictorial decription of diffusion imaging and postprocessing techniques. For further information, please see these references.

Diffusion MRI background

Diffusion is the random thermal motion of molecules. With MRI, we can measure the magnitude and direction of the diffusion of water molecules in vivo.
When there is oriented fibre structure, the diffusing water molecules will move preferentially in parallel to the fibre direction.
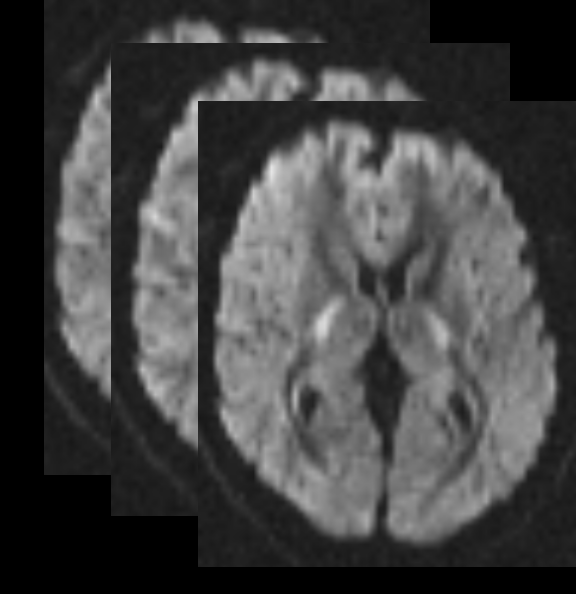
Diffusion Imaging involves acquiring a series of diffusion weighted images (DWIs) and from them inferring something about the underlying tissue structure. The diffusion displacement distribution, including magnitude and directional information, can be calculated from the DWIs.
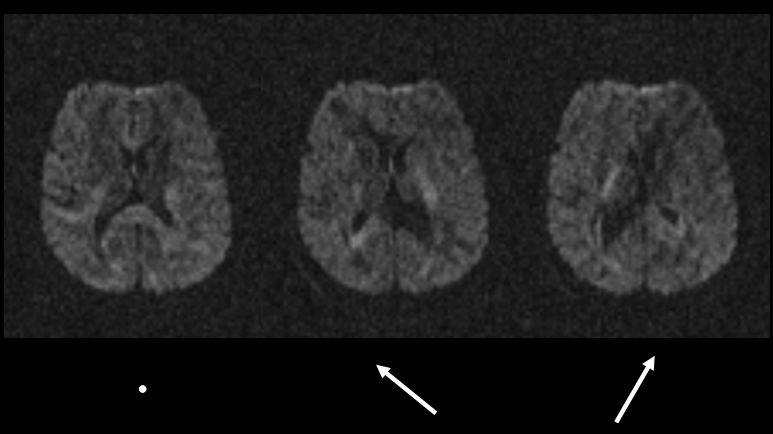A diffusion weighted image is one in which the signal intensity is decreased in the direction of an applied diffusion sensitizing gradient. Above, we see that the difference in the signal decreases when the diffusion sensitizing gradient is applied parallel or perpendicular to the white matter fibre tract direction.
Diffusion tensor imaging (DTI) is done by fitting the diffusion probability density function (PDF) to a 3D Gaussian function, which can be described with a second order tensor. The eigenvector corresponding to the largest eigenvalue of the diffusion tensor will lie along the direction of maximal diffusion.
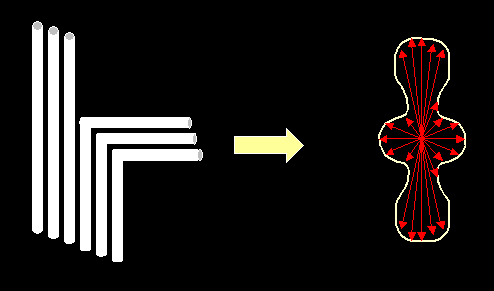
With the tensor model, it can be difficult to describe the fibre architecture in voxels in which there are multiple fibre directions. However, the diffusion PDF can be measured at high angular resolution to obtain information about multiple subvoxel fiber directions. There are a number of new methods that have been proposed for measuring the diffusion PDF at high angular resolution (HARD techniques). These include q-space methods such as diffusion spectrum imaging (DSI), persistent angular structure (PAS) reconstruction, multi-tensor reconstruction, and Q-ball imaging (QBI).
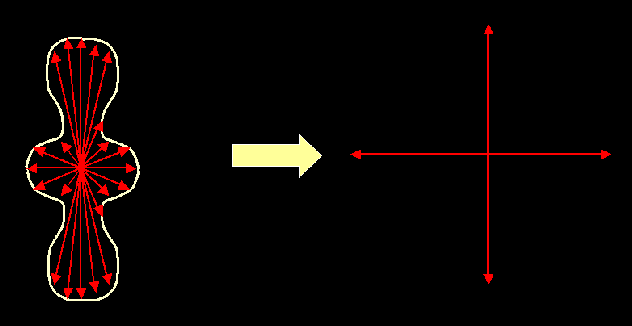From this diffusion PDF, we hope to infer the fibre orientation PDF. This can be done by simply extracting the maxima of the diffusion PDF, or by more sophisticated modeling and statistics.
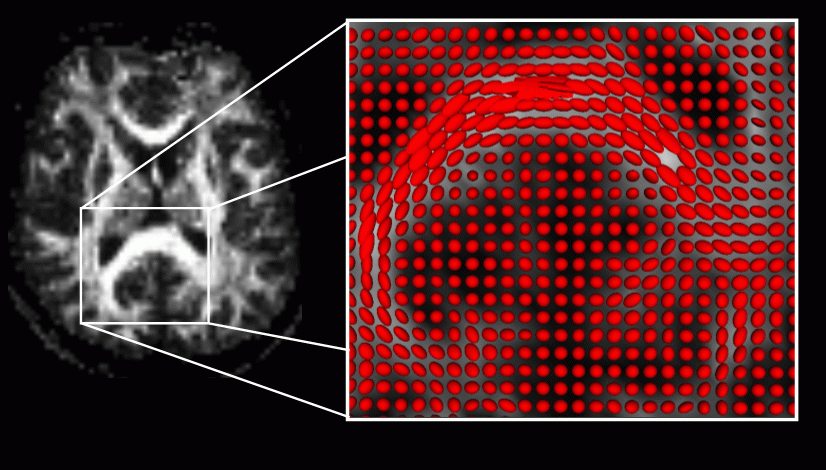Diffusion orientation distribution function (ODF), or projection of the diffusion PDF on the surface of the sphere.
Red-green-blue (RGB) map showing the direction of the principal eigenvector of the diffusion tensor.
The diffusion ODF shown in the region of interest outlined in the RGB map (far left). Left: QBI reconstruction. Right: DTI reconstruction. This ROI contains fibres from both the superior longitudinal fasciculus and the corpus collosum. The topmost ODF indicates that in some voxels, there is significant partial volume averaging of fibre directions, in which case the tensor model does not clearly show their directions.
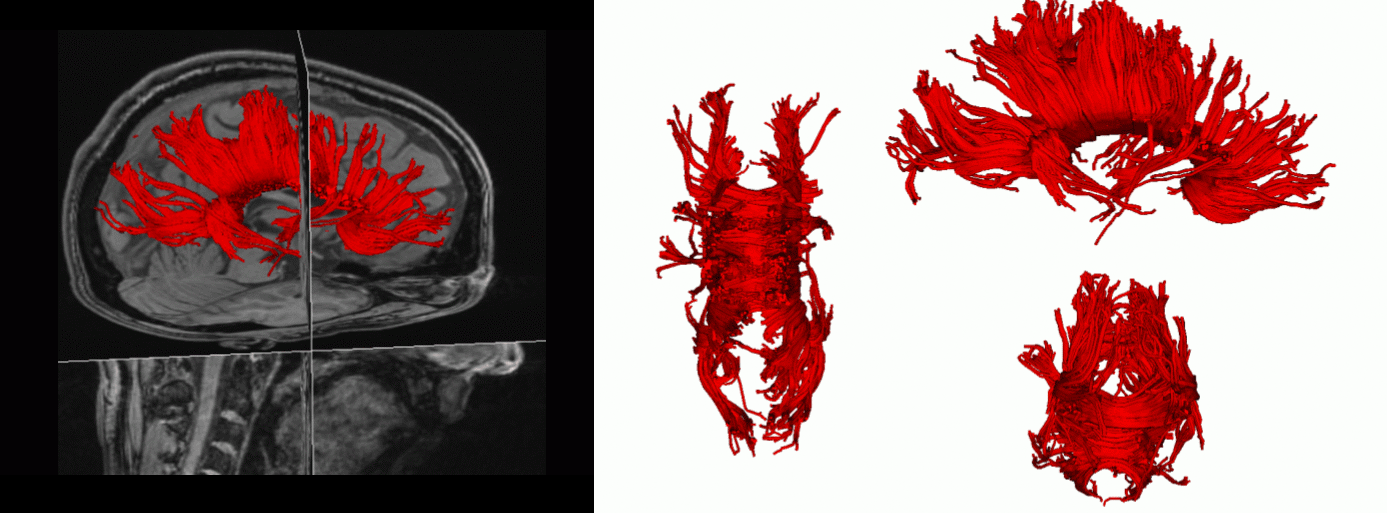Fibre tractography: tracts of the corpus callosum.
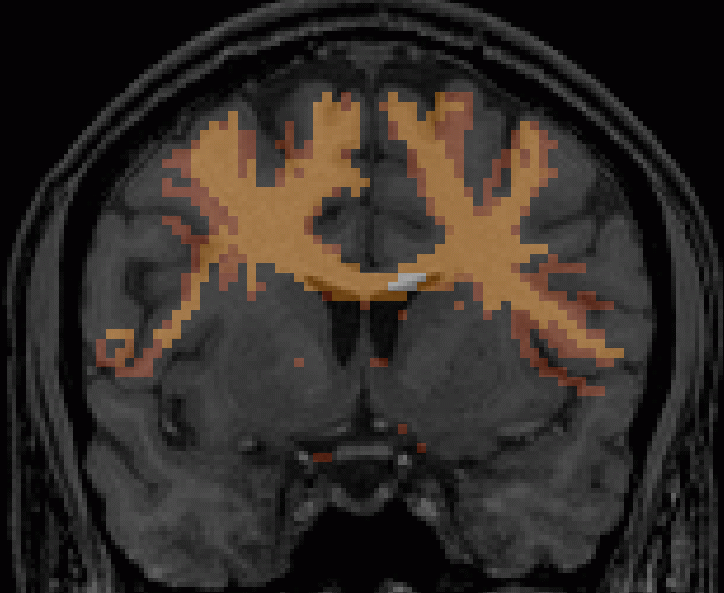
Maximum intensity projection (MIP) of uncertainty associated with fibre connections.

Projects