Complexity & Computability

Scott McCloskey

Research Paper

One of the more enduring and important problems in complexity theory, the "P/NP Conjecture", is still of great importance today. More than the theoretical implications that would result from its proof or refutation, the classification of problems by their minimal complexity class is would be helpful information for algorithm designers attempting to find efficient solutions to real-life problems. With or without this knowledge, though, it is important to be able to actually solve these problems at a reasonable expense (be it measured in time, hardware cost, or whatever dimension is needed). It is for this reason that alternate methods of computation have been formalized and, to a lesser extent, implemented to solve problems. One recent example of such a method is what is known as DNA computing, which attempts to solve these problems by taking advantage of the storage capacity of our genetic code. Since the field's genesis in 1994, the practice of DNA computing has grown significantly in both the number of problems that it might be used to solve and our understanding of its power. It is the purpose of this paper to describe DNA computing, from Adleman's initial experiments to the current state of the field, in order to get perspective on it's future viability. It is assumed that, before undertaking this paper, the reader has some familiarity with the basics of DNA, particularly the natural tendency of a strand and its complement to form the famous double helix structure of Watson and Crick.

The field of DNA computing is generally considered to have begun with Leonard Adleman's 1994 experiment involving the Hamiltonian Path (HP) problem. Simply stated, the HP problem is to determine whether or not a graph, with fixed starting and ending vertices, has some sequence of steps by which every vertex in the graph is visited exactly once. Formally, an instance of HP takes the form (V, E, s, d), where V and E are the sets of vertices and edges that define the graph's topology and s and d are the start and destination vertices. Adleman found a DNA algorithm by which one could determine, in linear time, whether or not such an instance belonged to HP (membership meaning that there is some path satisfying the criteria above). The choice of this problem is rather important in light of the fact that HP is known to be NP-complete, which is to say that any problem whose solution can be verified in polynomial time may be reduced to HP by some polynomial time algorithm. This is a truly remarkable result, as it shows that all problems in NP can be solved, by reduction, in polynomial time (due mostly to the reduction) by a DNA-based computer.

Adleman's algorithm for solving HP looks remarkable simple, and can be performed in linear time by the following steps (Adleman, 1):

1. Generate random paths through the graph
2. Remove those paths that begin with vertices other than s and those that end with vertices other than d.
3. Remove those paths that visit a number of vertices unequal to the size of the set V.
4. Remove those paths that visit some vertex more than once. (Note: this is the step that makes the overall algorithm execute in linear time. This step is a loop, executed once for each vertex, whose body goes about removing paths that contain that vertex more than once.)
5. If there are any paths left, answer "yes," otherwise "no."

Clearly these are fairly high-level steps, which should cause the reader to be skeptical about the claim that this can be performed in linear time. The first step, during which all of the paths through the graph are generated, would certainly translate to exponential complexity on a Turing-equivalent computing device. We will now discuss in detail how this particular step is performed by a DNA computer. The other steps, which would also be quite complicated to perform on a Turing machine, are discussed in greater detail in later sections.

In order to generate DNA sequences that represent all paths through the graph, one must first decide upon a DNA-based representation for the vertices and edges that comprise it. The design of the edges will follow the design of the vertices, so we choose to designate unique DNA strands for each vertex. The actual length of these strands depends, of course, on the size of the set V, and is chosen such that no two strands will have long common sub-strings. Were it not for this restriction, which will be explained in a later section, one could represent each of n vertices by a DNA strand of length log₄(n) (rounded toward infinity).

This leads us to defining the representation of the edges in the graph, where we will use, for the first time, the notion of a strand’s complement. Given some DNA strand, its complement is found by replacing all occurrence of A’s with T’s and vise versa, as well as replacing all instances of C’s with G’s and vise versa. Finally, each edge a->b will be represented by a strand (of the same length as the strands representing the vertices) whose first half will be the complement of the second half of the strand representing a and whose second half will be the complement of the first half of the strand representing b.

With this representation in mind, we create test tubes that have many multiples of the strands representing each edge and each vertex. Once these tubes are mixed together, legal paths through the graph are generated by the mutual attraction of strings and their complements by hydrogen bonding. For example, take the graph shown in figure 1.

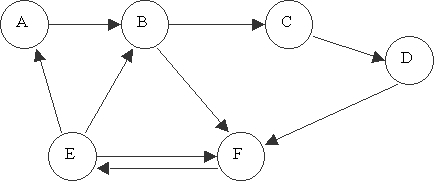Since this example has six vertices and the DNA alphabet only contains the letters A, T, C, and G, it is necessary to have each vertex represented by at least two characters. We expand this to eight characters in order to avoid the problem of long common sub-strings, and denote each vertex by a DNA strand as listed in table 1. The edges, furthermore, are represented as in table 1. Notice that the structure of the strands representing each edge follows from the strands representing the vertices as described above.

We can now see that, given this representation, strands representing vertex A in a test tube will tend to pair with strands representing edges of the form A -> x. Because of this tendency to pair, one can construct all paths through the graph by simply producing large quantities of each of the strands listed in table 1 and mixing them together. Other environmental conditions must be met so that the pairing process takes place as intended, but those details will be left for later discussions.

Once all of the legal paths are constructed, finding a solution (if one exists) to the instance of HP is equivalent to finding a double-stranded DNA sequence that contains exactly one copy of the strands representing each vertex. This search is exactly what is done in steps 2 through 5, and can be performed using methods from molecular biology. Moreover, each of these steps (including the synthesis of the paths) could be performed in linear time and thus the entire algorithm can be executed in linear time.

Adleman's initial experiment was performed on an instance of HP with seven vertices and relatively few edges. The algorithm successfully discovered the Hamiltonian path and was considered a success. In his concluding remarks, Adleman suggested that larger, more useful, instances of this problem could be solved simply by increasing both the length of the strands representing each edge and vertex, as well as increasing the number of copies of each strand used in the experiment.

This initial success created quite a bit of clamor in the computing community. Researchers began defining more and more algorithms to solve hard problems using DNA computing while others began to think about what a true "DNA computer" would look like. Furthermore, theoreticians began to question the true computing power of this new method, and whether or not it was truly a different paradigm of computation. Steps were also taken to formalize the operations that one could perform on a test tube full of DNA strands and how those steps would relate to traditional notions of Turing computability.

While a number of equivalent formalizations exist, we follow the descriptions from [2]. Note that the types of operations available are a result of the capability of molecular biology rather than the wishes of algorithm designers. Also note that these algorithms are performed in constant time (ignoring the variability of different technicians, etc) on test tubes which, for the sake of this discussion, may be of arbitrary size. These operations are as follows:

1. Merge - This is the simple operation of combining the contents of two test tubes in a third tube.
2. Anneal - This is the process by which complementary strands of DNA are paired to form the famous double-helix structure of Watson and Crick. Annealing is achieved by cooling a DNA solution, which encourages pairing. Adleman uses this in step 1 to generate all legal paths through the graph.
3. Melt - Melting is the inverse operation of annealing. By heating the contents of a tube, double-stranded DNA sequences are denatured, or separated into its two single-stranded parts.
4. Separation by length - The contents of a test tube can be separated by increasing length. This is achieved by gel electrophoresis, whereby longer strands travel more slowly through the gel. This operation was used by Adleman in step 3 of his solution to HP.
5. Separation by sequence - This operation allows one to remove from solution all DNA strands that contain a desired sequence. This is performed by generating the strand whose complement is the desired sequence. This newly generated strand is attached to a magnetic substance which is used to extract the sequences after annealing. This operation is the crux of Adleman's step 4.
6. Copying/Amplification - Copies are made of DNA strands in a test tube. The strands to be copied must have known sequences at both the beginning and end in order for this operation to be performed.
7. Append - This process makes a DNA strand longer by adding a character or strand to the end of each sequence.
8. Detect - It is also possible to analyze a test tube in order to determine whether or not it contains at least one strand of DNA. This operation, for example, is the last in Adleman's algorithm where we attempt to find a DNA sequence that has survived the previous steps.

In analyzing these operations, it becomes obvious that the power of DNA computing comes from its ability to perform the same operation simultaneously on the contents of a test tube. Since the duration of the operation does not depend on the size of the test tube, operations can be performed in parallel with no added cost. While it may seem that this parallelism is potentially unbounded, it should be noted that the restricting concern is that the volume of the test tubes must increase in order to accommodate more simultaneous computations. It almost seems, then, that the time complexity of NP problems solved by Turing machines is being traded for a type of volume complexity in DNA computing.

Noticing that DNA computing allows massive parallelism in constant time leads one to a comparison with quantum computing. Quantum computing, a topic of much recent research, performs parallel operations by means of a quantum register. Such registers, in a certain configuration, are thought to be in all possible states simultaneously. As a consequence of this, operations on this register can be thought of as being performed in parallel on all possible states of the register. The mechanisms of such registers, though beyond the scope of this report, allow one to extract the result corresponding to certain states in an attempt to find the answer to a specific computation.

The primary difference between DNA and Quantum computing, we see, is that DNA increases parallelism at the expense of additional volume (the contents of a test tube) while the quantum register allows these parallel computations to be performed in a fixed physical area. One other important distinction between the two is that they afford different levels of assurance. DNA computing generates solutions in a probabilistic manner, where any particular solution is generated with some probability based on the complex dynamics of the bonding process. By increasing the number of each strand in the initial solution, one can assume with reasonable certainty that all possible solutions will be constructed in the initial solution set. In quantum computing, by contrast, all solutions are guaranteed to be generated and we needn’t concern ourselves with the possibility of missing potential solutions.

Despite these differences, the similarities between these two methods are important to note. Most importantly, neither of these computing paradigms has been successfully implemented fully in an operational computer for public use. Secondly, the structure of algorithms for these two types of computer are fairly similar. The first phase typically involves the generation of all possible solutions to a problem and the second involves some method to extract the desired answer from all possibilities. This has been formalized by Claude and Paun [4] in the notion of solutions by carving.

As was previously mentioned, the initial publication of Adleman's groundbreaking experiment gave rise to a flurry of DNA-based algorithms for important problems. In addition to HP the satisfiability of logical formulas, another NP-complete problem, was solved using the methods of DNA computing. In addition to such classical problems, DNA computing has been used to show how one might break the DES encryption standard by means of a known plaintext attack [3]. In the discussion of cryptographic systems, a known plaintext attack is one where the person attempting to break the code is able to plant (and know the location of) some piece of text in the message before it is encrypted. The point of such an attack is for the eavesdropper to analyze a (plaintext, cyphertext) pair in order to determine the key that was used to encrypt the plaintext and, by extension, the entire message.

The attack is performed by starting with a test tube containing many copies of the (plaintext, key) pairs over all possible values of the key. DES, for example, has a 56-bit key, meaning that the initial solution would have at least 2⁵⁶ strands. DNA operations are performed on the test tube that mirror the DES encryption of that plaintext with the key specified by the value of the strand. At the end of the operation, which is also linear in time, the resultant test tube contains all (key, cyphertext) pairs derived from the known plaintext.

Given this test tube, then, the key can be found by extracting from it a strand that contains the cyphertext. Due to the way that it was constructed, the other half of this strand must contain the key used during the decryption, which can then be used to decrypt the entire message.

There are two important observations that should be made here. The first is that the test tube constructed in this process can be used to break multiple instances of DES so long as the same plaintext can be placed in the message. In the event that the message’s author detects that their encryption scheme has been broken, one reasonable course of action would be to change the encryption key. In this event, the eavesdropper could simply refer to the contents of the test tube in order to find the new key, which would be identified by the new cyphertext. This solution, then, would essentially act as a lookup table whereby keys can be found by simply searching for the corresponding cyphertext. The ability to re-use this solution for different keys helps to defray the initial cost of synthesizing the strands contained therein.

A second important observation is that this same type of algorithm can be used to break other types of encryption. The only constraint is that the encryption process needs to be implemented in terms of the DNA operations defined above. While DES has been broken by more conventional means, more secure encryption schemes may be susceptible to a DNA-based attack if the encryption mechanism can be carried out by DNA-based operations.

In addition to these practical results derived from DNA computing, a fair amount of attention has been paid to formalizing the computing power of a DNA-based system. One particular result (Beigel, 158) shows that the set of problems that can be solved in polynomial time with a DNA computer is equal to P^NP, the set of problems that can be solved in polynomial time by an oracle Turing machine M^SAT. Recall that M^SAT denotes a Turing machine that, during the course of its computation, can query the membership of a formula in SAT.

Note that, while this is an important result, it does not conclusively show that DNA computing is necessarily a different model of computing. If it turns out that P=NP then the Turing machine M^SAT must also be solvable in polynomial time and, by extension, all problems in P^NP must also be in P. Given the current algorithms for problems in NP, though, this result certainly indicates that DNA computing does provide a new type of computational power at the implementation level.

Since the boom in DNA computing research in the mid-1990's there has been a significant decrease in the number of technical papers and conferences related to the topic. An Internet search for DNA computing will direct the user to a number of sites, many of which haven't been updated in several years. What are some of the reasons for this precipitous fall from grace? It turns out that, while DNA computing provides a good theoretical framework within which to design algorithms, the ability to construct a DNA-based computer is limited by a number of implementation level problems.

The first problem, which has already been alluded to, has to do with the volume complexity that goes along with DNA computing. In his initial paper, Adleman speculated that more useful instances of the Hamiltonian path could be solved in linear time with a manageable volume of solution. Later analysis (Calude, 41) concluded that, due to the exponential growth of the number of paths with an increase in the number of vertices, the required mass of the solution for a graph with 200 vertices would exceed 3*10²⁵ kg! This is due, in part, to the fact that pairing of DNA strands in a test tube happens in a probabilistic manner, which requires that excess quantities be used in order to provide reasonable assurance that errors will be minimized.

While other algorithms may be more efficient in terms of volume complexity, the issues of scale are universally problematic for DNA computing. One contributor to this problem is the fact that strand pairing during the annealing process is subject to a whole host of errors. One of the more important errors occurs when two non-complementary strands are complementary over some long sub-string. Such strands are prone to pairing over those sub-strings where they are complements of one another, leaving the remainder as dangling ends in the solution. It is for this reason that, in Adleman’s experiment, unnecessarily long strands were used to represent each vertex in the graph. In general, when for example the number of vertices grows into the hundreds, selecting a large number of DNA strands that are sufficiently different from one another becomes a difficult problem.

One of the related problems with DNA computing is that there is no universal method of data representation. In today’s computer systems, for example, the binary representation is universally agreed upon. DNA computing, however, has no such standard. This is primarily due to the fact that there is no DNA-based operation to extract a strand if it has a particular value at a particular position. Extraction in DNA computing is performed solely be value and without respect to the value’s position within the strand, meaning that position information must be built into the sequence itself. This inclusion of positional information only exacerbates the problems of volume complexity outlined earlier.

What’s worse is that DNA-based representations of binary numbers are not extensible. Given a coding standard for an n bit binary sequence, extension to greater lengths generally requires that all of the DNA representations be regenerated in the form of longer strands to accommodate the additional information. This is a particularly annoying inconvenience, since it means that algorithm designers must explicitly design representation schemes for any problem before actually going about finding a solution.

Finally, one of the biggest problems facing the field of DNA computing is that no efficient implementation has been produced for testing, verification, and general experimentation. While Adleman’s initial experiment was performed in a lab, many of the subsequent algorithms in DNA computing have never been implemented or tested. The reason for this is that the resources required to execute these algorithms are both expensive and hard to find. Unlike common desktop computers, computing with a DNA-based solution has a high incremental cost both in the time of the operators and the raw materials that it uses. Were these facilities more available and affordable, real progress might be made in solving an interesting (large) instance of a problem using these new methods.

Despite all of the difficulties outlined above, there are still a number of researchers working on topics related to DNA computing. While they number fewer than in years past, much of their research seems to be motivated with a ground-up approach, focused on answering basic questions about DNA computing. Some more recent work has attempted to address the issues of data representation [5] and others with the ability to emulate today’s circuit-based computing in a DNA-based system.

It remains to be seen whether or not DNA computing will become a viable method of problem solving in the future, but it should be clear that the momentum of quantum computing continues to grow at the expense of DNA-based methods. As outlined earlier, the advantage of massive parallelism that makes DNA computing seem so beneficial would also be provided by a quantum computer, should one be built. It seems unlikely that a case could be made for continuing research in DNA computing, given all its inefficiencies, if a reasonable implementation of quantum computing could be made.

Despite its auspicious debut in 1994, it seems that DNA computing is destined to be remembered as a novel idea that was too difficult to implement practically. Much of the original hope surrounding the field had to do with the incredible data density that one could achieve with DNA, owing to the microscopic size of the sequences involved. That hope has since been limited by the reality that solutions to real life problems require, due in part to the probabilistic nature of the annealing process, many copies of each of the reactants. Overall it has been shown that the increases in the number of copies needed of each strand far outweighs the gains that one achieves by using DNA-based representations of data.

Despite the identified inefficiencies, it is certainly possible that in some instances a DNA-based computing system may prove to be the best solution. One could certainly imagine that the encryption-breaking method introduced above might become a viable solution for a highly motivated institution such as the military in a time of war. Any institution, for that matter, with sufficient motivation and access to the equipment and resources to undertake such a task might be well rewarded. What is less likely, however, is that DNA computing will become a replacement for electronic computing in the near future. Given the high cost and required space, it is hard to imagine the use of a DNA-based computer in many of the places where computers exist today; certainly the notion of including a DNA computer as part of a car’s control system is rather laughable.

Works Cited

1. Adleman, Leonard M. Molecular Computation of Solutions to Combinatorial Problems. Science, Vol. 266. November 11, 1994, Page 1021.
2. R. Beigel, and B. Fu. Solving Intractable Problems With DNA Computing. Proceedings of the Thirteenth Annual IEEE Conference on Computational Complexity, June 1998, Pages 154 - 168.
3. D Boneh, C. Dunworth, and R. J. Lipton. Breaking DES Using a Molecular Computer. Proceedings of the 1^st DIMACS Workshop on DNA Based Computers (1995). American Mathematical Society, 1996.
4. C. Claude and G. Paun. Computing with Cells and Atoms in a Nutshell. Complexity, Vol. 6, no.1 Pages 38-48
5. A. Condon, R. Corn, and A Marathe. On Combinatorial DNA Word Design. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, Pages 75-90 (2000). Available at http://corninfo.chem.wisc.edu/writings/DNAcomputing.html