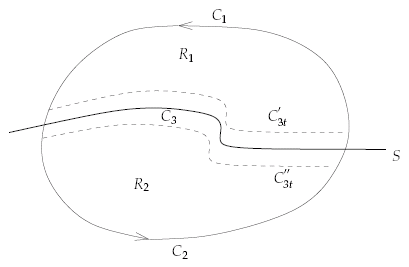
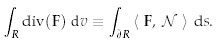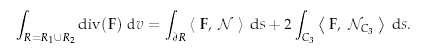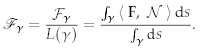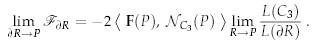Flux Invariants for Shape
Pavel Dimitrov	James N. Damon	Kaleem Siddiqi

Abstract

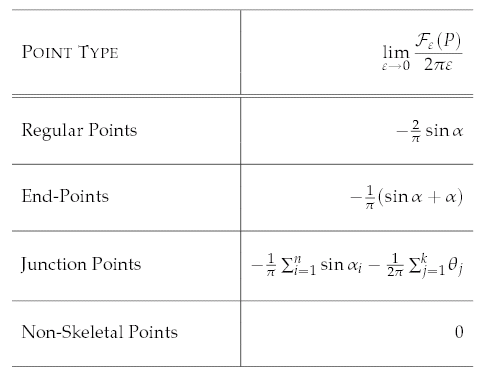
We consider the average outward flux through a Jordan curve of the gradient vector field of the Euclidean distance function to the boundary of a 2D shape. Using an alternate form of the divergence theorem, we show that in the limit as the area of the region enclosed by such a curve shrinks to zero, this measure has very different behaviours at medial points than at non-medial ones, providing a theoretical justification for its use in the Hamilton-Jacobi skeletonization algorithm of [SBTZ]. We then specialize to the case of shrinking circular neighborhoods and show that the average outward flux measure also reveals the object angle at skeletal points. 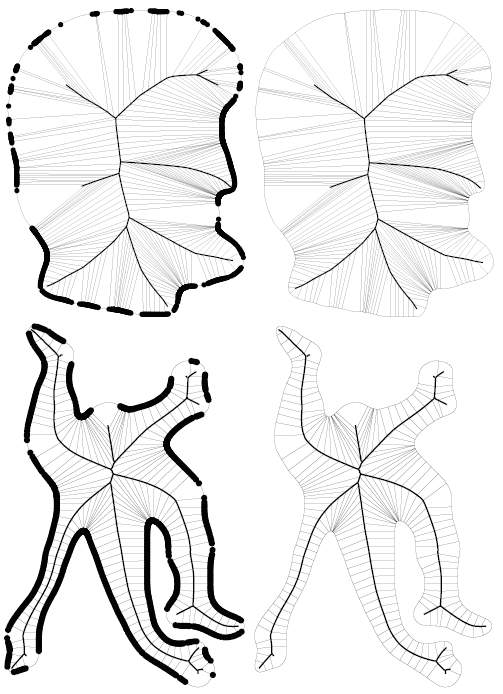Hence, formulae for obtaining the boundary curves, their curvatures, and other geometric quantities of interest, can be written in terms of the average outward flux limit values at skeletal points. Thus this measure can be viewed as a Euclidean invariant for shape description: it can be used to both detect the skeleton from the Euclidean distance function, as well as to explicitly reconstruct the boundary from it. We illustrate our results with several numerical simulations.

Keywords:	shape,skeletonization, medial axis, divergence theorem, flux map, distance map

Flux and Divergence
Circular Neighborhoods

Results

Experiments
References

Flux and Divergence

Definition. A 2D shape X is a is a subset of the real plane such that:

it is the closure of a bounded connected open set;
and the boundary of X consists of a finite number of mutually disjoint closed curves. Each boundary curve does not self-intersect and is composed of finitely many real analytic curve segments.

Definition. The Euclidean distance function induced by a shape X is defined

for a point P inside X, as the negative shortest distance from P to the boundary of X;
for a point P outside X, as the positive shortest distance from P to the boundary of X.

The Divergence Theorem applied to the gradient of the Euclidean distance function induced by a 2D shape (denoted F) takes the following form:

Divergence Theorem. Let X be a shape and let R be a path-connected region where div(F) is defined. Then, the total divergence of F over R is equal to the outward flux through the boundary of R, i.e.

where dv is an area element.

Figure 1. Region R of the plane containing a skeleton curve segment.

This result may be extended to include regions of the plane which include a curve segment of the skeleton; see Figure 1.

Theorem 1. For a path connected region R which contains part of a skeletal curve S, the divergence of the vector field F is related to its flux through the boundary of R by the following equation

Now consider the region R as it shrinks to a point P. It turns out that by normalizing the flux through the boundary of R, we may obtain a criterion which identifies P as either belonging to the medial set or not. This measure is called the average outward flux (AOF) and is obtained by dividing the flux by the Euclidean length of the boundary of R, i.e.

Using Theorem 1, we show that the limit of the AOF through a shrinking region is given by

Circular Neighborhoods

In the special case when R is a circle shrinking to a point by simply decreasing the radius, the limiting behavior of the AOF may be explicitly computed. It turns out that this limit provides much more than the expected binary information (skeletal/non-skeletal point) -- it relates regular skeletal points to their generating boundary points. Figure 2 defines (by example) the different types of skeletal points and Table 1 summarizes the results.

Figure 2. Types of skeletal points.

Results

Table 1. Flux values in the limit as a circular neighborhood shrinks to a point P.

Experiments

Figure 3 shows an experiment performed in order to corroborate the theory. The skeleton was obtained by first approximating the AOF through a very small discrete circle everywhere on a lattice and by performing a two-stage thinning based on the AOF values (noting that values near zero suggest non-skeletal points, see [Di] for a more detailed description). Then, the object angle (alpha) for regular points was estimated using the result in Table 1 thus enabling us to reconstruct the two corresponding boundary points.

Figure 3. Bi-tangent points associated with regular skeletal points: (LEFT) computed using average outward flux information (see Table 1) and (RIGHT) computed explicitly.

References

[Bl]	H. Blum. Biological shape and visual science (part 1). Journal of Theoretical Biology, 38:205--287, 1973.
[DDS]	P. Dimitrov, J. N. Damon and K. Siddiqi. Flux Invariants for Shape. In Computer Vision and Pattern Recognition, 2003, v. 1, pages 835--841. IEEE Computer Society, June 2003.
[Di]	P. Dimitrov. Flux Invariants for Shape. M.Sc. thesis, School of Computer Science McGill University, 2003.
[SBTZ]	K. Siddiqi, S. Bouix, A. Tannenbaum and S. W. Zucker. Hamilton-Jacobi skeletons. International Journal of Computer Vision, 48(3):215--231, 2002.

Pavel Dimitrov
Last Update: November 09, 2003.