Shape Analysis Group
Medial Axis Computation for Polyhedra
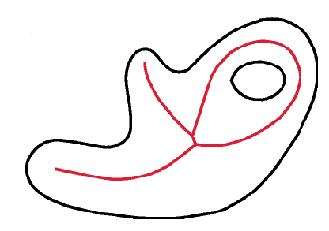
An interesting way to desribe a shape is as follows. Suppose that, at a particular instance in time, we light the entire boundary of the shape on fire. Suppose that the fire fronts travel in the direction of the inner normal to the boundary. If we were to note the locations inside the shape where two fire fronts meet, this collection of points represents the medial axis of the shape. For example, for the shape with the boundary shown in black in the figure below, the medial axis is the red curve.
The medial axis is homotopic to the original object. Furthermore, the original boundary can be reconstructed by taking the union of balls whose centres are the medial points and whose radii are the distance from the ball's centre to the closest point on the shape's boundary.
When the shape is 3-dimensional, the medial axis consists of surfaces and is a very complicated object that is hard to compute exactly. Moreover, knowing the complete medial axis may not be useful.
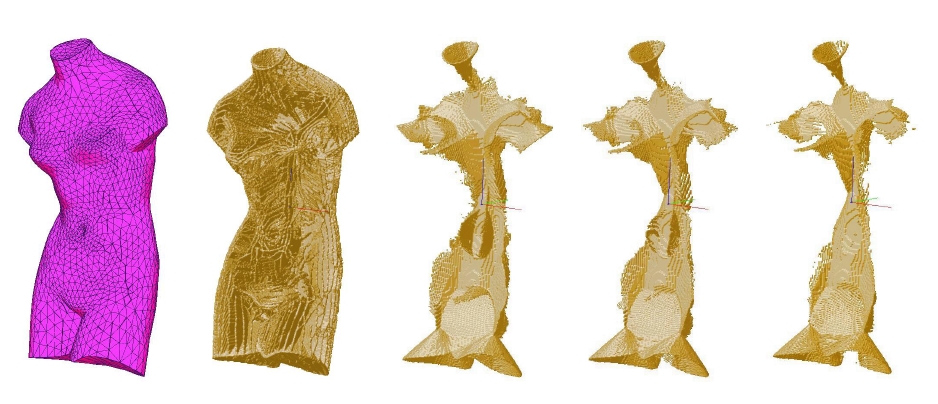
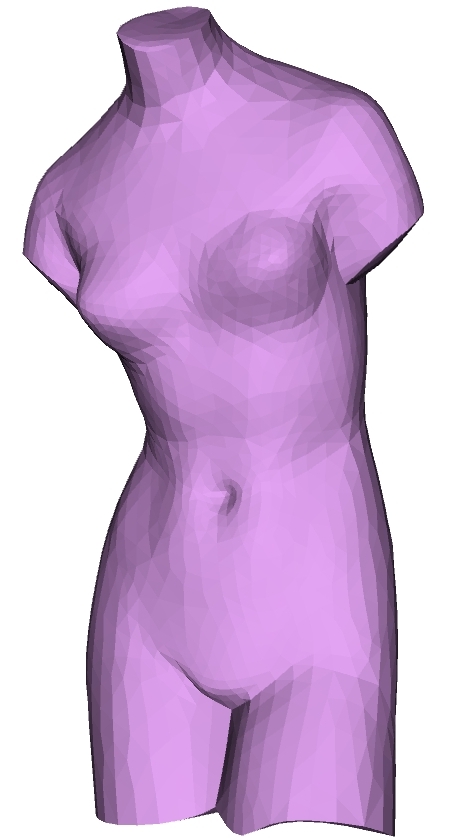
We have designed a sound algorithm that computes significant locations on the medial axis of a polyhedron. The figure below illustrates the voxels that contain parts of the medial surface for the ''Venus'' polyhedron, where the significance threshold is increased from left to right.
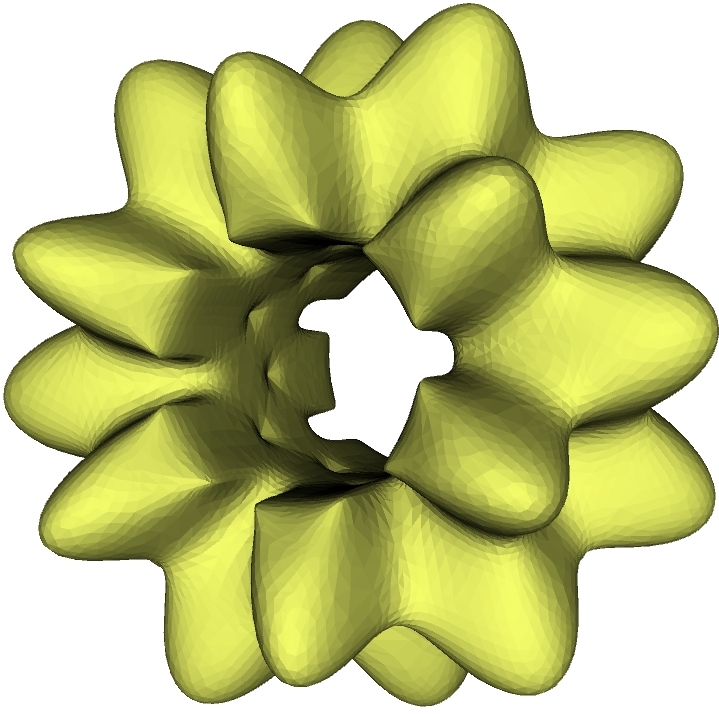
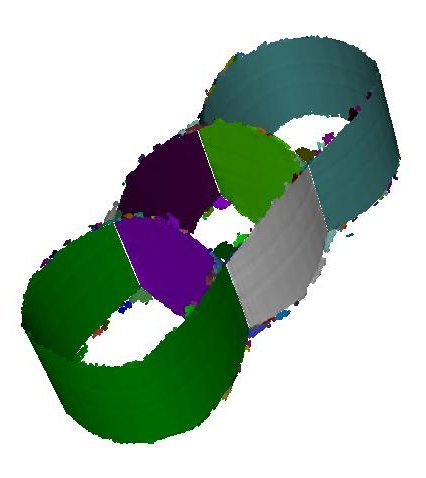
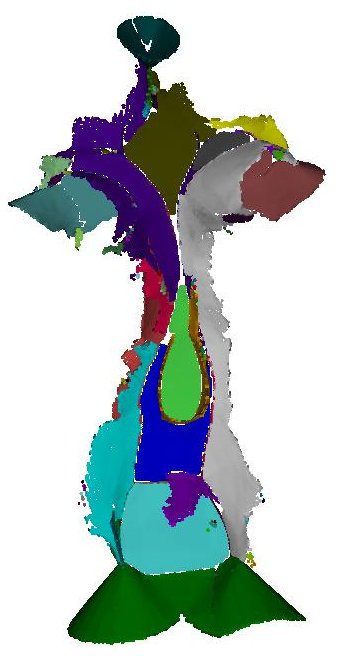
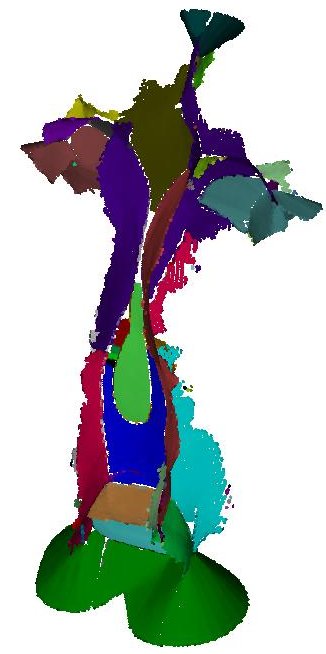
Not only can we find the set of voxels that contain the medial surface, we may also find for each voxel a point that lies within &epsilon of the medial axis and partition the set of these medial points into those that lie on distinct smooth sheets. Here are some examples of meshes and their significant medial points segmented into sheets:
Related Publications
S. Stolpner & K. Siddiqi.Revealing Significant Medial Structure in Meshes.
3rd International Symposium on 3D Data Processing, Visualization and Transmission (Chapel Hill, NC), 2006.
[ PDF] © 2006 by IEEE.