



Next: reduceLB
Up: Function Reference
Previous: simpLB
Contents
A possible alternative name for this function is collectLB.
Purpose
Regroup (collect) summands in an expression in terms of its Lie
brackets. The only properties applied are the distributivity over the
Lie products and the distributivity over scalar multiplication. The
anti-symmetry and Jacobi identities are not applied, however
(cf. reduceLB instead). Neither reduces the terms to a form in
the PHB, to this end use instead reduceLB, which is more
powerful, but obviously requires a PHB.
|
Syntax
p:=regroupLB(x);
Description
The command regroupLB groups together brackets which are equal,
in other words the scalar parts collected in terms of their common Lie
bracket; i.e. the underlying properties applied are that of
distributivity over the Lie products and over the scalar
multiplication. The command invokes simpLB to obtain the
scalar part and the pure (simplified) Lie bracket, the scalar parts
multiplying equal brackets are summed and expressed as a new factor of
the corresponding simplified Lie bracket (the common factor). This
function is mostly based on finding like members in a list and
conceptually simple, thus no further algorithmic details will be
included.
|
Arguments

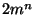
Note
The regroupLB does not apply the anti-commutativity or
anti-symmetry property, neither the Jacobi identity. To reduce an
expression to its simplest (shortest) form, use reduceLB, which
is more powerful in the sense that it takes into account the
anti-symmetry and Jacobi properties, however it requires the
specification of a PHB.
|
Examples
First consider as a simple example the following:
> z:=f0&*f1+(u0_1*f0)&*f1;
z := (f0~ &* f1~) + (f0~ u0_1~ &* f1~)
> regroupLB(z);
(1 + u0_1~) (f0~ &* f1~)
As a second, more complex example, consider the linear combination of
vector fields f_1, f_2 and f_3 given in the
example for the function createLBobjects on
page ![[*]](file:/usr/share/latex2html/icons/crossref.png) . And let . And let z:=f_1&*(f_2+f_3);,
then
|
> z:=f_1&*(f_2+f_3);
z:=(f0~ u0_1~ &* f0~ u0_2~) + (f0~ u0_1~ &* f1~ u1_2~)
+ (f0~ u0_1~ &* f2~ u2_2~) + (f0~ u0_1~ &* f0~ u0_3~)
+ (f0~ u0_1~ &* f1~ u1_3~) + (f0~ u0_1~ &* f2~ u2_3~)
+ (f1~ u1_1~ &* f0~ u0_2~) + (f1~ u1_1~ &* f1~ u1_2~)
+ (f1~ u1_1~ &* f2~ u2_2~) + (f1~ u1_1~ &* f0~ u0_3~)
+ (f1~ u1_1~ &* f1~ u1_3~) + (f1~ u1_1~ &* f2~ u2_3~)
+ (f2~ u2_1~ &* f0~ u0_2~) + (f2~ u2_1~ &* f1~ u1_2~)
+ (f2~ u2_1~ &* f2~ u2_2~) + (f2~ u2_1~ &* f0~ u0_3~)
+ (f2~ u2_1~ &* f1~ u1_3~) + (f2~ u2_1~ &* f2~ u2_3~)
> regroupLB(z4);
(u0_1~ u0_2~ + u0_1~ u0_3~) (f0~ &* f0~)
+ (u0_1~ u1_2~ + u0_1~ u1_3~) (f0~ &* f1~)
+ (u0_1~ u2_2~ + u0_1~ u2_3~) (f0~ &* f2~)
+ (u1_1~ u0_2~ + u1_1~ u0_3~) (f1~ &* f0~)
+ (u1_1~ u1_2~ + u1_1~ u1_3~) (f1~ &* f1~)
+ (u1_1~ u2_2~ + u1_1~ u2_3~) (f1~ &* f2~)
+ (u2_1~ u0_2~ + u2_1~ u0_3~) (f2~ &* f0~)
+ (u2_1~ u1_2~ + u2_1~ u1_3~) (f2~ &* f1~)
+ (u2_1~ u2_2~ + u2_1~ u2_3~) (f2~ &* f2~)
The latter example clearly shows that only the distributivity over
scalar multiplication is applied, since terms like (f0~ &* f0~)
are not made zero, neither factors of, for example, (f0~ &* f1~)
and (f1~ &* f0~) are collected together.
|
Implementation Notes
The first implementation of this function suffered of some memory
problems, due to some problem in the way Maple handles the memory of
sequences and lists. A work around this problem was to transform the
list into an array and back into a list to eliminate certain elements
in a simple ways using the subsop function from Maple. The
details can be found in the source code.
|
It's worth to mention that for larger control systems and models,
memory limitations might occur even if memory is formally
allocated with the functions to declare arrays, especially if a high
order CBH formula (cf. cbhexp, p. ![[*]](file:/usr/share/latex2html/icons/crossref.png) ) is
employed. A possible approach to face memory related obstacles is to
decrease the order of the CBH used. The exponent returned by
cbhexp is a sum of approximately ) is
employed. A possible approach to face memory related obstacles is to
decrease the order of the CBH used. The exponent returned by
cbhexp is a sum of approximately 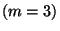 brackets, where brackets, where 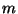 is
the number of generators, is
the number of generators, 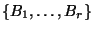 the order of the CBH formula employed.
For example, in the case of three generators the order of the CBH formula employed.
For example, in the case of three generators 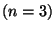 and a third order
CBH and a third order
CBH 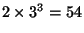 , the CBH exponent would have more than , the CBH exponent would have more than 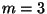 elements in the sum. For the case of of
elements in the sum. For the case of of  and and 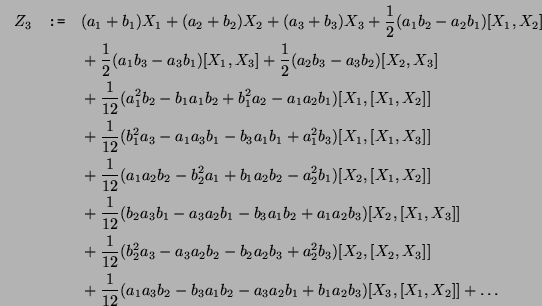 the number of
elements increases drastically to more than 162, actually the number
of summands is 231 when the elements of order smaller than 4 are taken
into account. the number of
elements increases drastically to more than 162, actually the number
of summands is 231 when the elements of order smaller than 4 are taken
into account.
|




Next: reduceLB
Up: Function Reference
Previous: simpLB
Contents
Miguel Attilio Torres-Torriti
2004-05-31
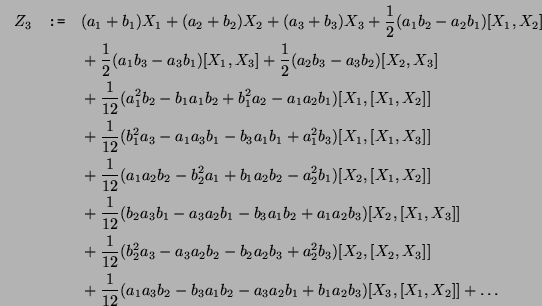 the number of
elements increases drastically to more than 162, actually the number
of summands is 231 when the elements of order smaller than 4 are taken
into account.
the number of
elements increases drastically to more than 162, actually the number
of summands is 231 when the elements of order smaller than 4 are taken
into account.