PATTERN RECOGNITION

Course Project for cs644 A Simple Method for Computing General Position in Displaying Three-Dimensional Objects (Paper by Tomihisa Kamada and Satoru Kawai, 1987) #Abstract #Introduction #Method #Algorithm #Applet #Conclusion NOTE: THE APPLET WORKS WITH INTERNET EXPLORER BUT NOT NETSCAPE4 FOR SOME REASON (sad but true..I guess ie won this one)

1.0 Abstract

The following is an implementation of a method proposed by Kamada and Kawai in their paper to compute the "nicest" viewing angle for a 3D wire frame object. This viewing angle is "nice" as it is intended to provide the viewer with the maximum shape information.

2.0 Introduction

The projection of a 3D image onto a 2D canvas is controlled by parameters such as the View Reference Point (VRP), the View Up vector (VUP), the View Plane Normal (VPN), the Center of Projection (COP) (in perspective projection) and the projection direction (in parallel projection). The VRP is a point on the projection plane which when combined with the VPN define the projection plane. The VUP vector is another axis orthogonal to the VPN along the projection plane. Ultimately one has to choose the VRP such that one obtains the desired visual effects and obtains the shape of the objects being viewed. Kamada and Kawai present a method of choosing the VRP in such a manner that the general appearance of the objects in view is easily obtainable. The term general here means that the shape information of the original 3D objects is represented to the maximum extent on a 2D plane. For example, we want a cube to be seen as a cube and not a square upon projection to a 2D plane.

3.0 Method

The method described in the paper is applicable only to parallel projections where the projection direction is perpendicular to the projection plane. The problem of finding the VRP thus resorts to computing the projection direction vector.

Consider projecting a line in 3D onto a 2D plane. If the projection results in a point, all the information about the line is lost. This happens when the projection direction is parallel to the line. Similarly for two lines in 3D, the worst case happens when both lines are projected onto a single line in 2D. This happens when the projected direction is parallel to the plane containing the two lines. This worst case scenario can be avoided however by the non-zero angle between the projection direction and the plane. In fact, the greater the angle is, the more geometry regarding these two lines can be understood in the resultant projection. See diagram below (top half).

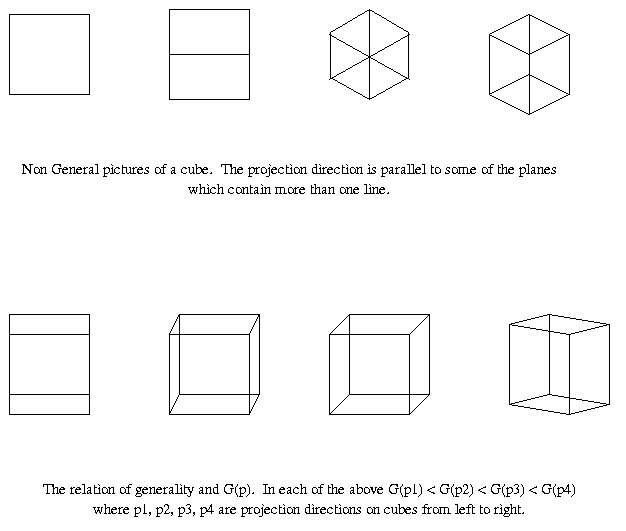FIGURE 1 depicts cubes seen from non general views (top) and general views (bottom)

DEFINITION 1: Let L be the set of lines of an object
DEFINITION 2: Let T be the set of unit normal vectors of the planes which contain more than one element of L. Note that this is does not say the set of normals for the faces.
DEFINITION 3: Let p be the unit vector of the projection direction which we want to compute.

The idea behind the paper is precisely to compute this vector p.

DEFINITION 4: Let G(p) = min(|p.t|) ,where t is an element of T, be the generality measure of a vector p.

Since p and t are both unit vectors above, their dot product is merely the cosine of the angle between them. So if you compute the angle between all the vectors t in T and p, G(p) expresses the cosine of the maximum angle between p and t as the smaller the cosine of an angle, the larger that angle (NOTE the absolute value).

In order to maximize the generality of the most non general parts, the maximin criterion is used. It can be said that the larger G(p) is, the more general p is (see diagram above, bottom half). This is true as the value of G(p) increases, the maximum angle between p and t becomes smaller; in other words the minimum angle between p and planes which contain more than one line becomes larger.

We seek the most general vector that maximizes G(p). Hence the general position problem can be reduced to the maximin problem of determining p which maximizes G(p), i.e.,

max min (|p.t|) where |p| = 1 and t is an element of T

3.1 Algorithm

Consider taking all the normals from T (note that these are not just the normals of the faces of the wire frame object but also include normals to any plane containing two or more edges) and joining them such that they all originate at the same point. The tips of these normals all lie on the surface of the unit sphere. So the problem of finding p can be viewed as the problem of finding the smallest circle on a unit sphere that encloses all of t or -t where t is an element of T. The unit vector p which maximizes G(p) is located precisely at the center of this circle. By examining this unit sphere from a view directly incident onto the center of this computed circle (i.e. looking down into the sphere along the line drawn from the center of the sphere along p to the camera) the viewer is guaranteed to see the most t's, and hence have the best impression of the wire frame image.

If a unit vector p maximizes G(p) then there are at least two elements t₁ and t₂ which satisfy

G(p) = |p.t₁| = |p.t₂| This is due to the fact that the smallest enclosing circle problem goes through at least two or three points on the surface of the unit sphere. When its goes through only two points, the line joining these two points is the diameter of the circle.

The algorithm is therefore:

Compute all enclosing circles and their respective centers
Find the smallest circle from these, the center of which gives desired p

More formally follow the algorithm link to see the full algorithm (taken verbatim from the paper)

4.0 Applet

The applet works in the following manner:

Given an input file consisting of points and edges, it proceeds to compute p and map the 3D wire frame onto the 2D awt canvas. The points are specified as: pt label x,y,z where the user is free to choose the label, and x,y,z are the coordinates of the point. NOTE: since no bounding box is used in the projection, values of points which fall beyond the size of the canvas will not be drawn. This is not a severe restriction as the canvas is large. Once the points are inputted, edges have to be specified to connect the points. An edge is specified in the following manner: edge label1 label2 where label1 and label2 conform to the labels of two inputted points.
Once the wire frame is constructed, the applet proceeds to find all the normals T. Once all the normals are there, p is computed from them and the wire frame is mapped to a 2D plane specified by p. Note that the camera is always placed looking into the wire frame down the line drawn from the center of the wire frame along the direction specified by p. Once a 2D parallel projection is obtained, it is drawn onto the canvas

Using the applet:

To run the demos click the choices button and choose one of the demos. Once the demo is chosen the user can enter (into the small text field by the buttons) any view thats been precomputed e.g. if 30 views are computed the user can enter any view number from 0 to 29. Since the algorithm is O(n⁴) the more complicated the wire frame in terms of the number of normals computed, the longer it takes. For the star please be very patient as it takes a few minutes.
To input your own wire frame, first enter the points into the text field provided (using the format given above) then enter the edges (using the format given above). Once everything is entered, click the compute button. Note that to see what you have entered, type show into the text field and see the result in the java console provided by your browser. This process can be very tedious so another alternative is to mail me the file of the wire frame you wish to see and I can add it to the demos.
The rotate button obviously rotates the wireframe. It does so in a manner such that the entire object is seen. The stop rotation button kills the rotate thread whereas the pause one suspends the thread.
If you want the source code please mail me.

5.0 Conclusion and future work

Needless to say the algorithm is very slow. However it can be modified to a more complicated algorithm which works in O(n³) on average and O(n³ *log n) in worst case.

Stay tuned to see the next version which will show all the best views computed (as p is not necessarily unique) as well as giving the user the ability to choose progressively better/worse views. Also a spinning wire frame which halts to give the best view would be nice.

6.0 Acknowledgments

Thanks to Professor Godfried Toussaint who helped decipher the algorithm and taught the course superbly. Also thanks to Richard Unger who effectively taught me this Java thing and provided the command parser for text input for the code.